易坊好文馆

  1. 首页 > 生活百科 >

AI 算法的进化：机器会引发战争吗？( 二 )


大家都知道 ， Netflix公司是一家会员订阅制的流媒体播放平台 ， 开发出自己的电影推荐系统后 ， 在2006年举办了奈飞大奖赛 ， 期望通过竞争来发掘最优的算法 。当时 ， Netflix已经积累了大量的电影评级数据 ， 评分等级分为1~5星 。于是 ， 它公开了一个包含100 480 507个元素的电影评级训练集合 ， 这些元素取自480 189个用户对17 770部电影的评价 。然后 ， Netflix将17 770部电影的名称替换为数字序号 ， 即变为匿名状态 。比如 ， 2666代表的可能是《银翼杀手》 ， 也可能是《安妮·霍尔》 ， 或其他任何一部影片 。只有用户给这部电影的评分是已知的 。
同时 ， Netflix还公布了一个包含2 817 131个元素的测试集合 。测试集合的用户对电影所做的评价是未知的 ， 因此参赛队提交的算法必须预测测试集合中所有的元素所对应的评价等级 。比如 ， 根据已有的数据预测出用户234654对2666这部影片的评价等级 。重赏之下必有勇夫 ， 公司宣布设立100万美元奖金作为奖励 ， 获奖条件是：以推荐效率提高10%的优势击败Netflix的自有算法 。附加条件是：获胜者必须公开自己的算法并授予公司非排他性的许可 ， 让Netflix有权使用这个算法向用户推荐电影 。
除了100万美元的终极奖项 ， 大赛还设立了几个进步奖：将上一年度成绩最好的推荐算法的效率提高至少1%的团队 ， 将获得进步奖50 000美元 。该奖项每年度都会有 ， 但领取奖金的前提条件依然是需要公开算法的代码 。
可能你会觉得从这样的数据里得不到有价值的信息 ， 因为你甚至不知道2666所代表的影片是喜剧片还是科幻片 。事实上 ， 原始数据所蕴含的信息远比我们想象的要多 。假设我们将每部电影视为一个维度 ， 所有影片就构成了一个17 770维度的空间 ， 那么每个用户就可以被看作这个17 770维空间中的一个点 。每一部电影对应一个维度 ， 用户对影片的评价越高 ， 那么在该维度上此点偏离原点的距离就越远 。当然 ， 除非你是一个数学家 ， 不然把用户看作17 770维空间中的点是很难想象的 。实际上 ， 我们可以把高维空间看作三维空间的扩展 。假定只有3部影片被评级 ， 我们可以用图形化的方式将用户与影片评级的关系表示出来 。
假设电影1是《狮子王》 ， 电影2是《闪灵》 ， 电影3是《曼哈顿》 。某一用户对这三部影片的评级分别为1星、4星和5星 。用x、y、z轴表示用户对电影1、电影2、电影3的喜爱等级 ， 建立三维空间直角坐标系 ， 如图6-1所示 。这时 ， 我们可以确定该用户在坐标系中的位置是（1 ， 4 ， 5） 。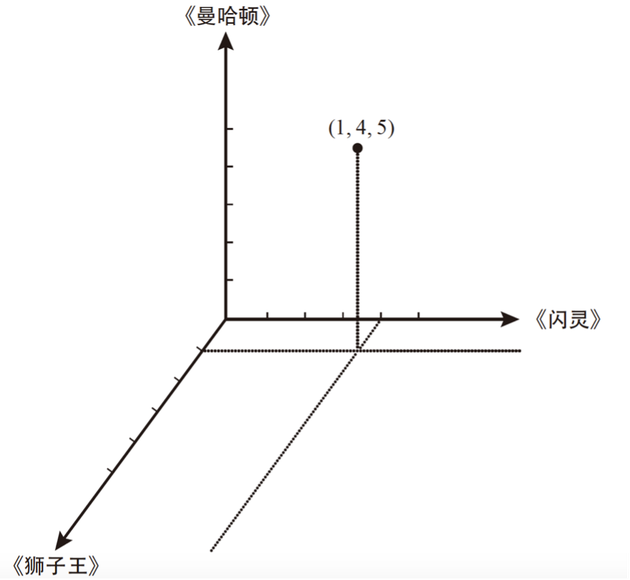
AI 算法的进化：机器会引发战争吗？
文章图片

图　6-1
虽然在几何上无法绘制出17 770维空间以呈现用户在该空间上的所在位置 ， 但数学可以 。如果能把用户看成17 770维空间中的点 ， 那么同样能把影片看作480 189维（用户数）空间中的点 ， 此时 ， 如果用户对影片评价越高 ， 那么在该维度上此点偏离原点就越远 。这些点分散在如此之大的维度中 ， 很难发现其间存在的模式 。因此 ， 如果希望借助计算机找出数据中包含的信息 ， 那么就需要降维处理 。
这就好比一系列从不同角度得到的某人的头部剪影 ， 其中一些更具代表性 ， 更容易辨识一样 。比如 ， 希区柯克（Hitchcock）的侧影轮廓就比正面投影更易辨认 。电影和用户就像脸上一个一个的点 ， 以一个角度投影 ， 可能会看到这些点连成一条线 ， 而以另外的一个角度投影 ， 则可能并不会发现有明显的信息出现 。
按照这个思路 ， 我们或许能找到一种办法 ， 将高维空间中的电影和用户对应的点同时投射到一个二维平面上 ， 这样用户对应的点就会非常接近他喜爱的电影所对应的点 。这种办法的巧妙之处就在于 ， 能够寻找到揭示影片、用户所具有的潜在特征的合适投影 。例如 ， 图6-2是100个用户和500部电影匹配过后在二维平面中的投影 ， 所使用的数据均来自Netflix的数据库 。代表用户的点与代表影片的点很好地拟合 ， 其余各处均未出现异常多余的点 。我们可以通过这个投影找到数据中的信息 。

推荐阅读


上一篇：中国侨网 福建追回“红通人员”30人！原副局长自述外逃捡废品为生16年

下一篇：数字货币 数字货币这轮大跌像极了上一轮