易坊好文馆

  1. 首页 > 生活百科 >

黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释( 二 )

如果我们继续解析u和v，这些关系将适用于所有的史瓦西黑洞时空。
为了得到史瓦西黑洞的Kruskal-Szekeres图，我们引入了两个新的坐标，即：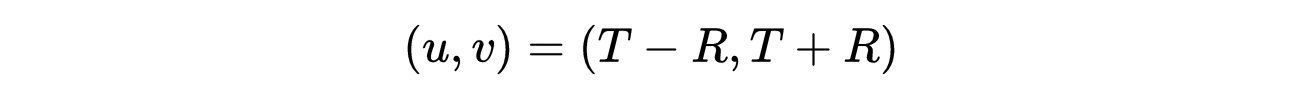
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图

  • 式7：坐标u和v的定义。
现在，为了覆盖整个图，我们必须扩展坐标(u, v)。用原始坐标(t, r)表示扩展变量(u, v)，我们得到两组坐标，即：
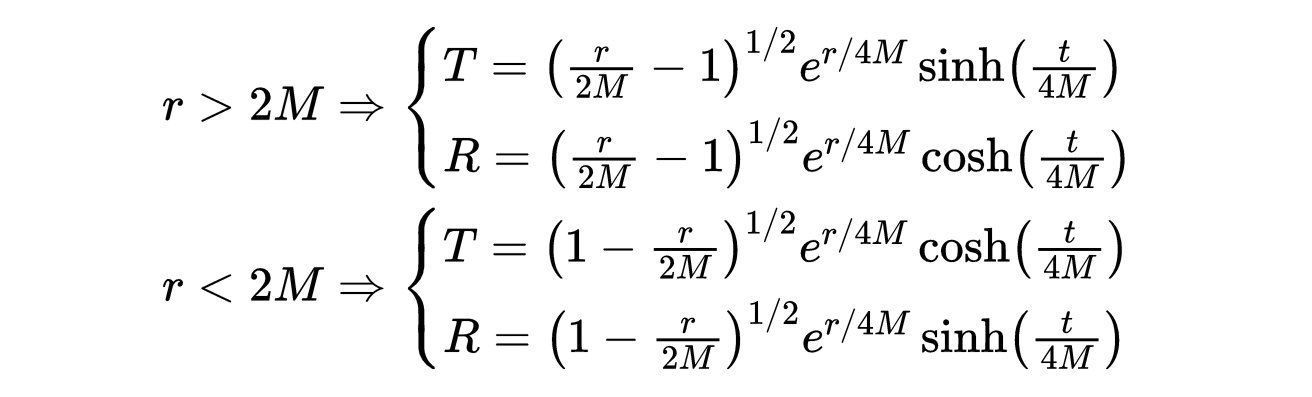
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式8：史瓦西黑洞几何上的两组Kruskal-Szekeres坐标。上对坐标覆盖黑洞外部(r >2m)，下对坐标覆盖黑洞内部(r
Kruskal-Szekeres图如下图所示：
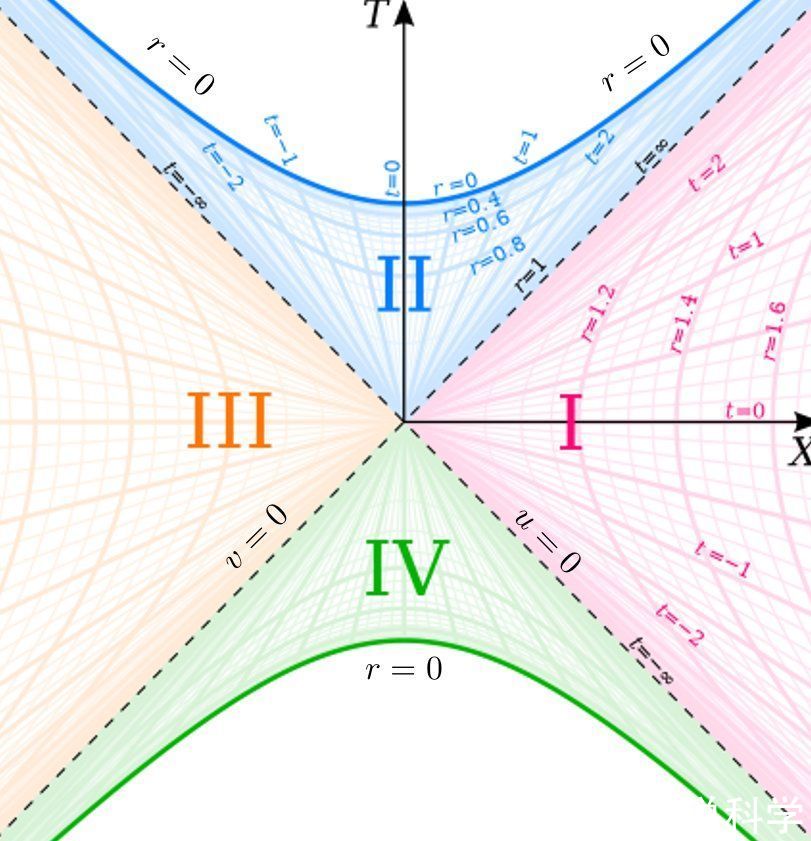
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 图5：Kruskal-Szekeres图，其中轴为坐标(T, R)。史瓦西黑洞时空被划分为四个渐近区域I, II, III, IV。R为常数的曲线为双曲线，T为常数的线为直线
请注意以下几个重要特征：
  • 我们知道(u,v)零测地线是斜率为π/4和-π/4的直线
  • 由式6可知，超曲面r = const对应于T-R平面上的下列双曲：
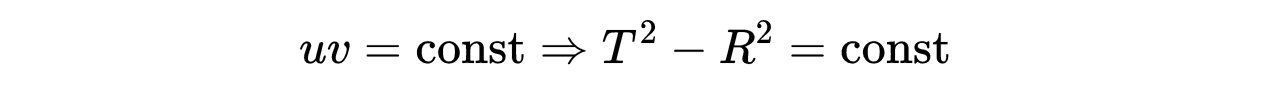
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式9
由式6，对于r > 2M，我们有uv 0，这意味着方程9中的双曲线r =常数是类时间的。对于r < 2M则相反，uv > 0，式9中的双曲线r =常数是类空间的。
从等式6的第二个表达式中，我们可以看出，曲面t =常数是用直线表示的。 对于r 2M（在黑洞内部），时间t变成了空间坐标。在外面，t仍然被解释为时间。降维说，在事件视界内，空间和时间有效地互换了!
在T的两个值处有两个奇点：
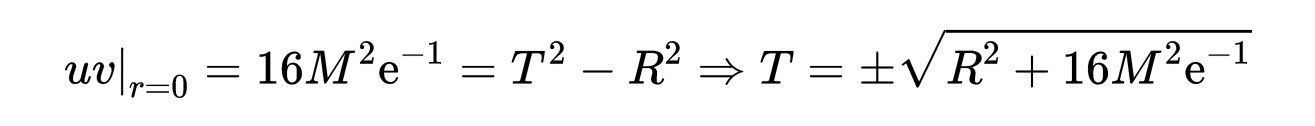
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式10：r=0对应的两个类空间奇点。
两个r = 0曲面以外的区域不能被这些坐标覆盖。
量化【 黑洞|为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释】为简单起见，让我们写出二维弯曲时空中无质量标量场的作用：
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式11：具有度规张量g的二维弯曲时空中无质量标量场的作用。
对应于S的标量场方程可以用tortoise光锥坐标或Kruskal-Szekeres光锥坐标表示。在这两种情况下，它都是两项的和：
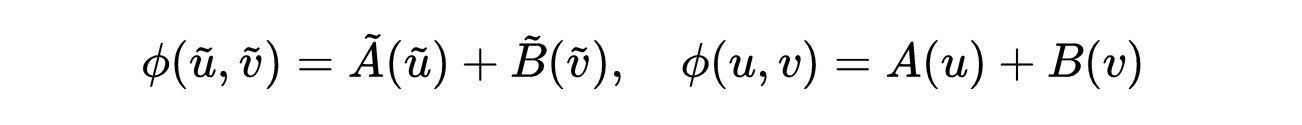
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式12：上述作用S对应的标量场方程，用tortoise光锥坐标和Kruskal-Szekeres光锥坐标表示。
这是S的正形不变性的结果。a和b是行为良好的函数。下面是一个简单的例子：
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
用tortoise光锥坐标表示的史瓦西线元素为：
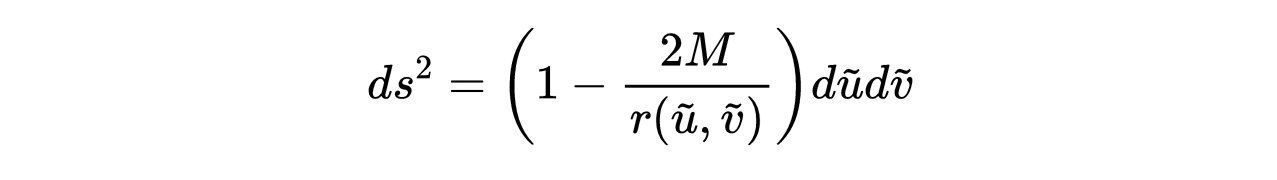
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式14：史瓦西线元，用tortoise光锥坐标表示。
在离黑洞很远的地方，线元素变成：
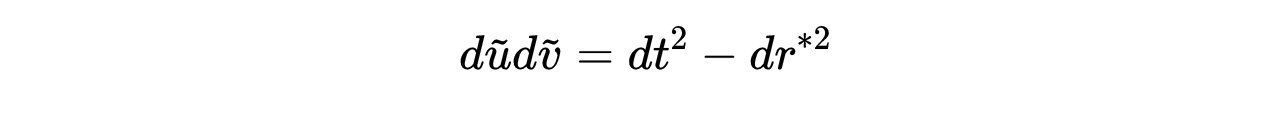
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式15
我们看到，在离黑洞很远的地方，静止观察者的固有时间与式15中的t重合。
在量子场论中，我们通常用创造和湮灭算符来扩展场：
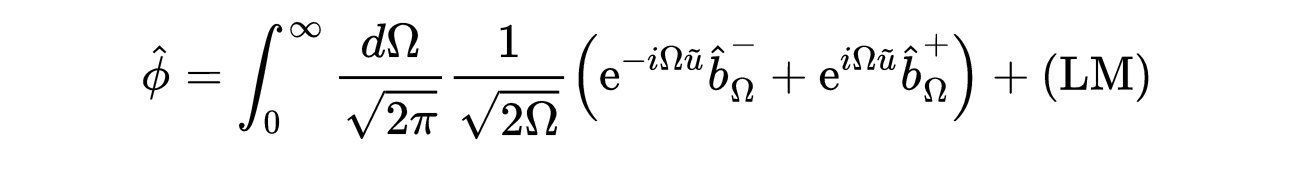
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式16：场?的扩展。
对应于b湮灭算符的真空称为Boulware真空，根据距离黑洞很远的观察者的说法，它不包含任何粒子：
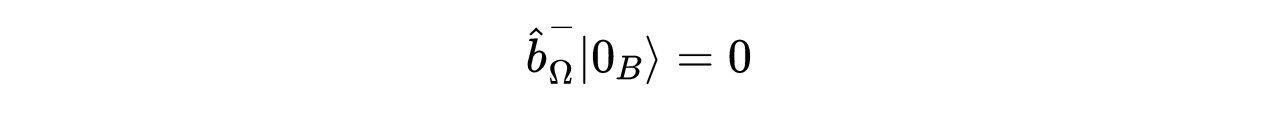
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式17：Boulware真空。
因为，正如我们之前看到的，tortoise光锥坐标只覆盖了史瓦西黑洞时空的一部分（视界外），Boulware真空在视界上有奇异的行为，因此它在物理上是无效的。此外，相应的能量密度会在视界处发散，量子涨落会产生强烈的反向反应，从而推翻弱扰动经典引力场的基本假设。
与tortoise光锥坐标相比，Kruskal-Szekeres光锥坐标覆盖了所有的史瓦西黑洞时空，并且在视界上定义明确。在视界附近，Kruskal-Szekeres坐标中的线元素为：
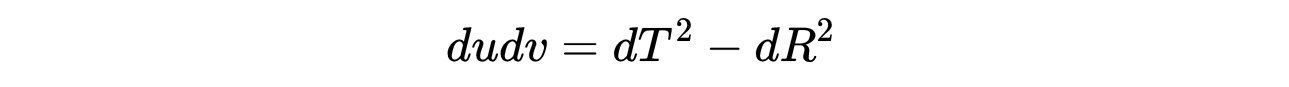
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图
  • 式18：视界附近的Kruskal-Szekeres光锥坐标中的线素。
因此，一个穿过视界的观察者与一个频率为ω > 0的模式有关。再次如式16所示扩展场，我们得到：
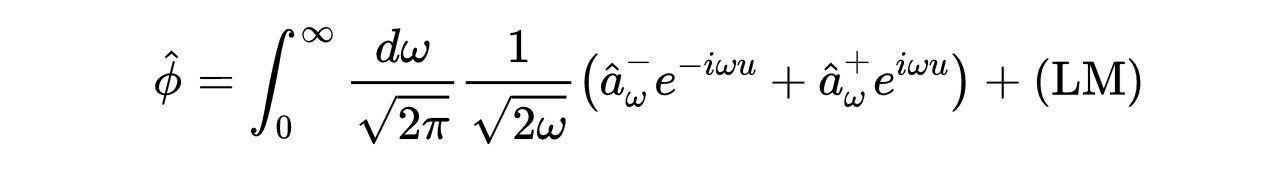
黑洞 为什么黑洞会发光？霍金辐射背后的物理学，最硬核的解释
文章插图

上一篇：塔斯马尼亚 时隔三千多年，袋獾再次在澳洲大陆实现自然繁殖

下一篇：太阳系 就只知道比邻星太阳系的邻居不止这一个，这些或许你没听过