贝叶斯公式的最通俗解释

文章图片

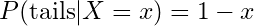
文章图片

文章图片

文章图片

本质上，贝叶斯公式描述了在给定新信息的情况下如何更新我们的模型。
为了理解原因，我们将看一个简单的例子：用不公平的硬币抛硬币。假设我们有一个神奇的硬币！抛掷时可能出现正面或反面，但概率不一定相等。问题是，我们不知道确切的概率。因此，我们必须进行一些实验和统计估计才能找到答案。为了数学地表述这个问题，我们用 x 表示正面朝上的概率。
我们对 x 了解多少？ \uD83E\uDD14
此时，什么都没有。它可以是 0 到 1 之间的任何数字。
贝叶斯先验与其将 x 视为一个固定数字，不如将其视为对实验 X 的观察。为了模拟我们对 X 的（缺乏）知识，我们选择 [0 1
上的均匀分布。这被称为先验，因为它表达了我们在实验之前的知识。
先验分布的密度，以概率形式表达我们对 X 的了解。
所以，假设我们已经扔了我们的魔法硬币，这次得到的结果是反面。它如何影响我们的硬币模型？
我们可以说，如果正面的概率是某个 x ，那么我们的实验导致反面的可能性是 1-x 。
注意，我们想知道条件和事件的概率分布:我们对参数的概率模型很感兴趣，因为这是我们之前的实验的结果。这被称为后验分布。
现在让我们把所有东西放在一起！
贝叶斯公式：先验后验贝叶斯公式正是我们所需要的，因为它用先验和似然来表达后验。
这可能令人惊讶，但实验产生反面的真实概率是无关紧要的。
为什么？因为它与 X 无关。另外，因为我们谈论的是概率分布，后验积分的计算结果为 1：
这里，反面的概率为 0.5 ，正如总概率定律所暗示的那样：
（在一般情况下，像这样的积分很难进行分析评估。）
所以，我们有我们的后验分布！请注意，它更集中在 x = 0 附近。（回想一下， x 是正面朝上的概率。）
换句话说，这意味着如果我们只看到一次抛硬币导致反面，我们猜测硬币偏向于此。
当然，我们可以进行越来越多的抛硬币，这可以进一步完善后验。在 k 个正面和 n-k 个反面之后，后验将是所谓的 Beta 分布。
总结这是最简单的贝叶斯公式解释了。
后验概率正比于先验概率乘以似然函数
或者，换句话说，贝叶斯公式描述了在给定新观察结果的情况下如何更新我们的模型。
因此，它在概率、统计和机器学习中起着基础性的作用。例如，这就是著名的均方误差的来源！
【|贝叶斯公式的最通俗解释】本文作者：Tivadar Danka

贝叶斯公式的最通俗解释

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)