元素的互异性具体应用，真没那么简单（详解含参方程解集）

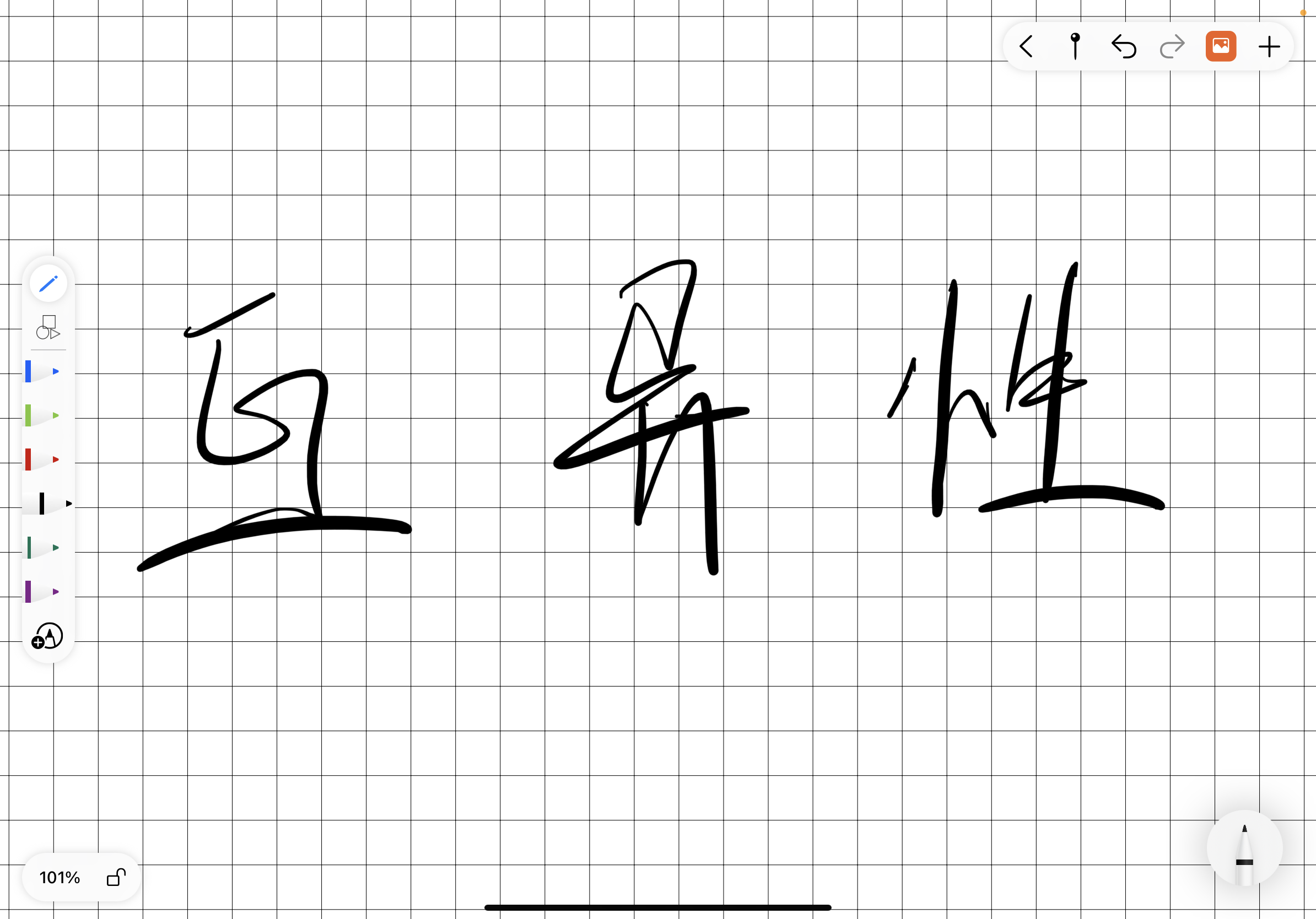
文章图片

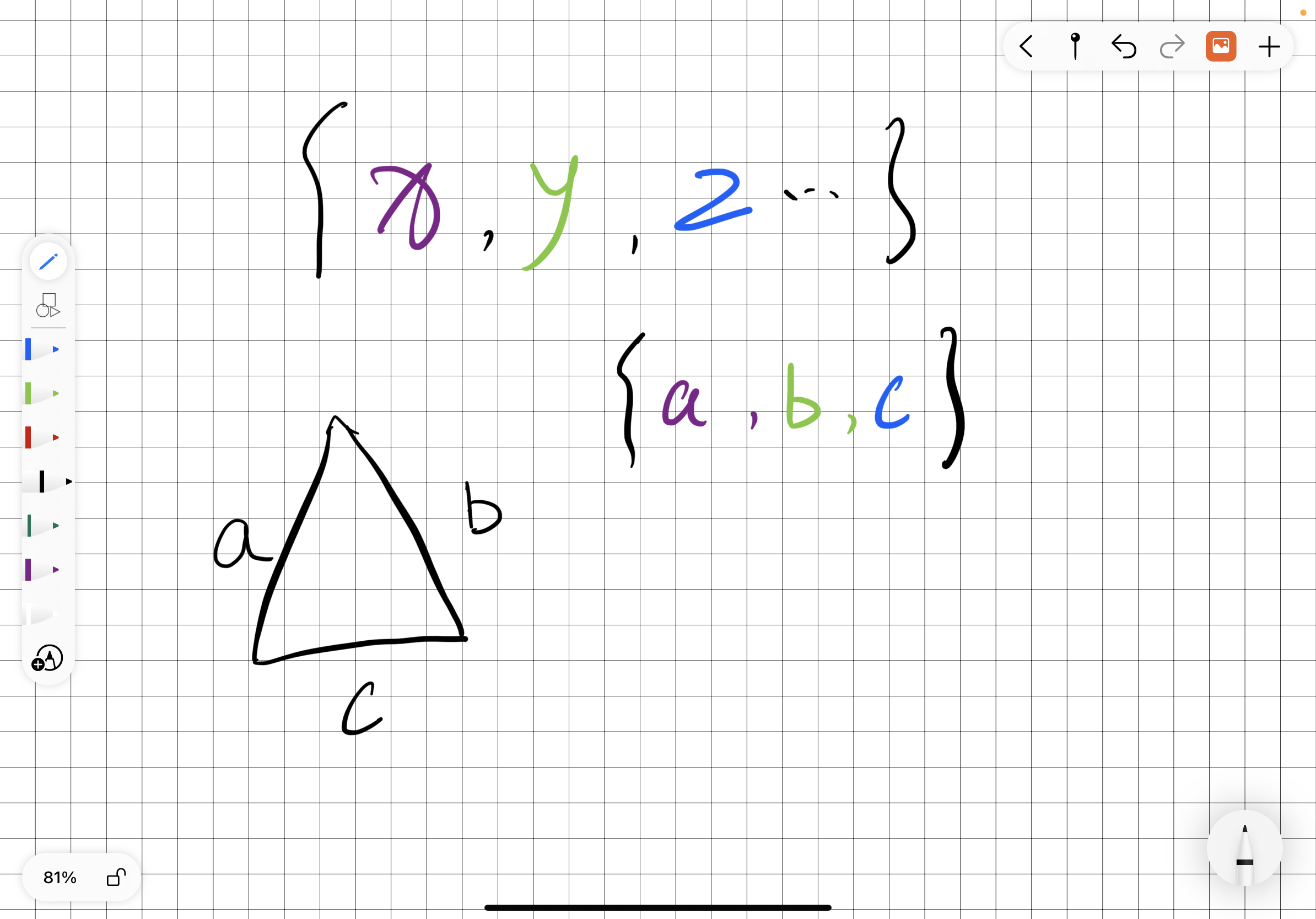
文章图片

文章图片

文章图片

文章图片

“平常的知识点，不一样的讲解，今天我们给大家带来第4节课《元素互异性的具体应用》，所谓互异性，就是集合中的元素互不相同”
方程互异性我们先来看一个简单的例子，比如我们写出图中方程的解集，虽然这个方程的两个根都是2 ，但是根据元素的互异性，再写解集时，这两个只能写一次。
但是如果反过来，如果集合中的元素都一个个列出来了{x ， y ， z ，那么你就应该立马想到，这些元素一定互不相同。
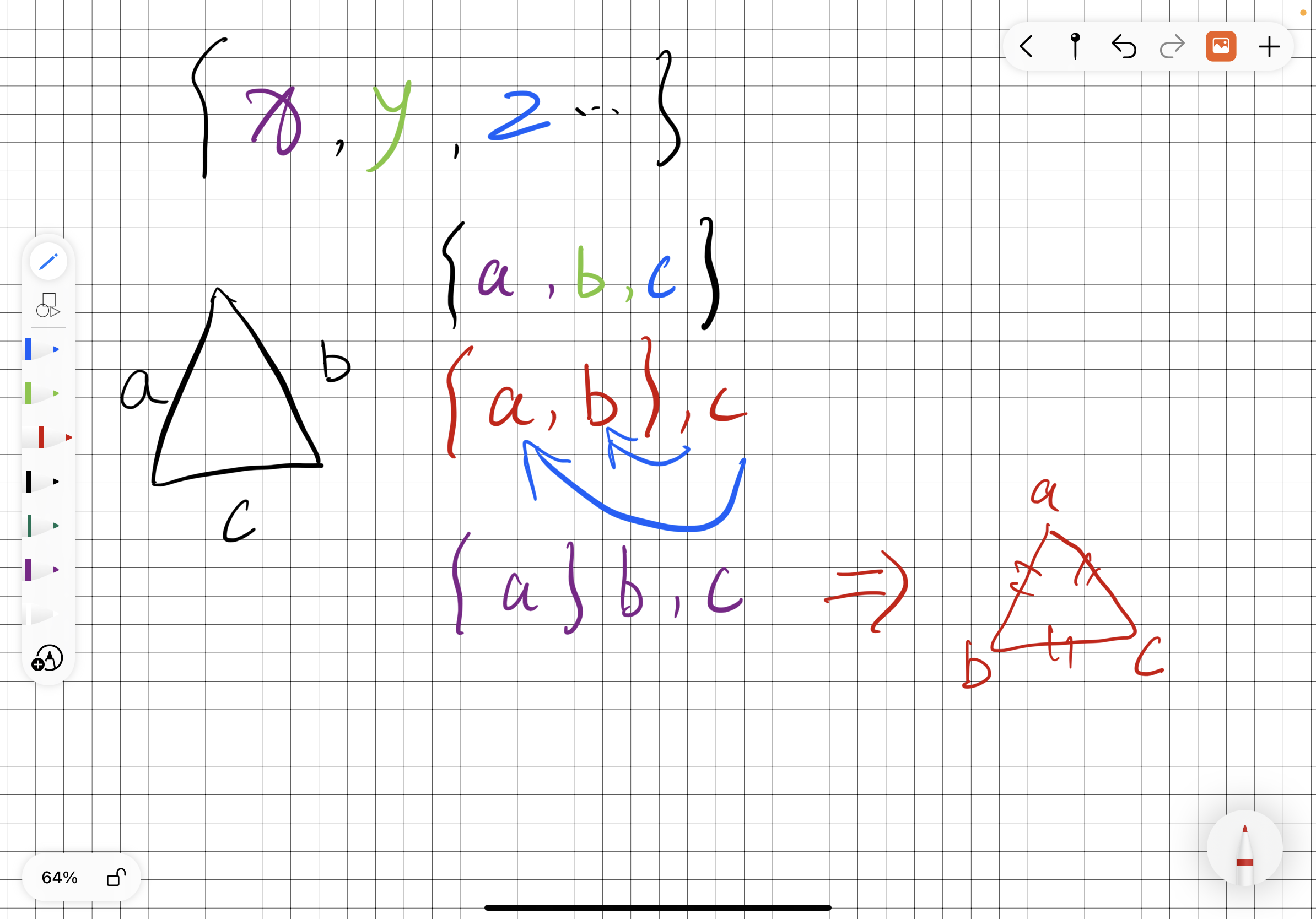
几何互异性上边说到，如果元素一个个都列了出来，那么这几个元素一定是互不相同的，那么我们再看下图，给你一个三角形，三边的集合为{a ， b ， c ，那么通过这个条件你就可以知道，这三边互不相等，因为把a ， b ， c放在一个集合中就注定他们互不相同。
那么如果三边长度的集合为下图的{a ， b ，你又能得到什么结论呢？既然c在集合中不出现，那说明c和{a ， b中的某一个一定相等。
如果我们再极端一点，集合中只有a ，也就是{a ， b ， c ，那就说明这是一个等边三角形。
以上的互异性用几何方式是很直观的，直接观看图形就可以明白，那么接下来我们要讲解代数的互异性了。
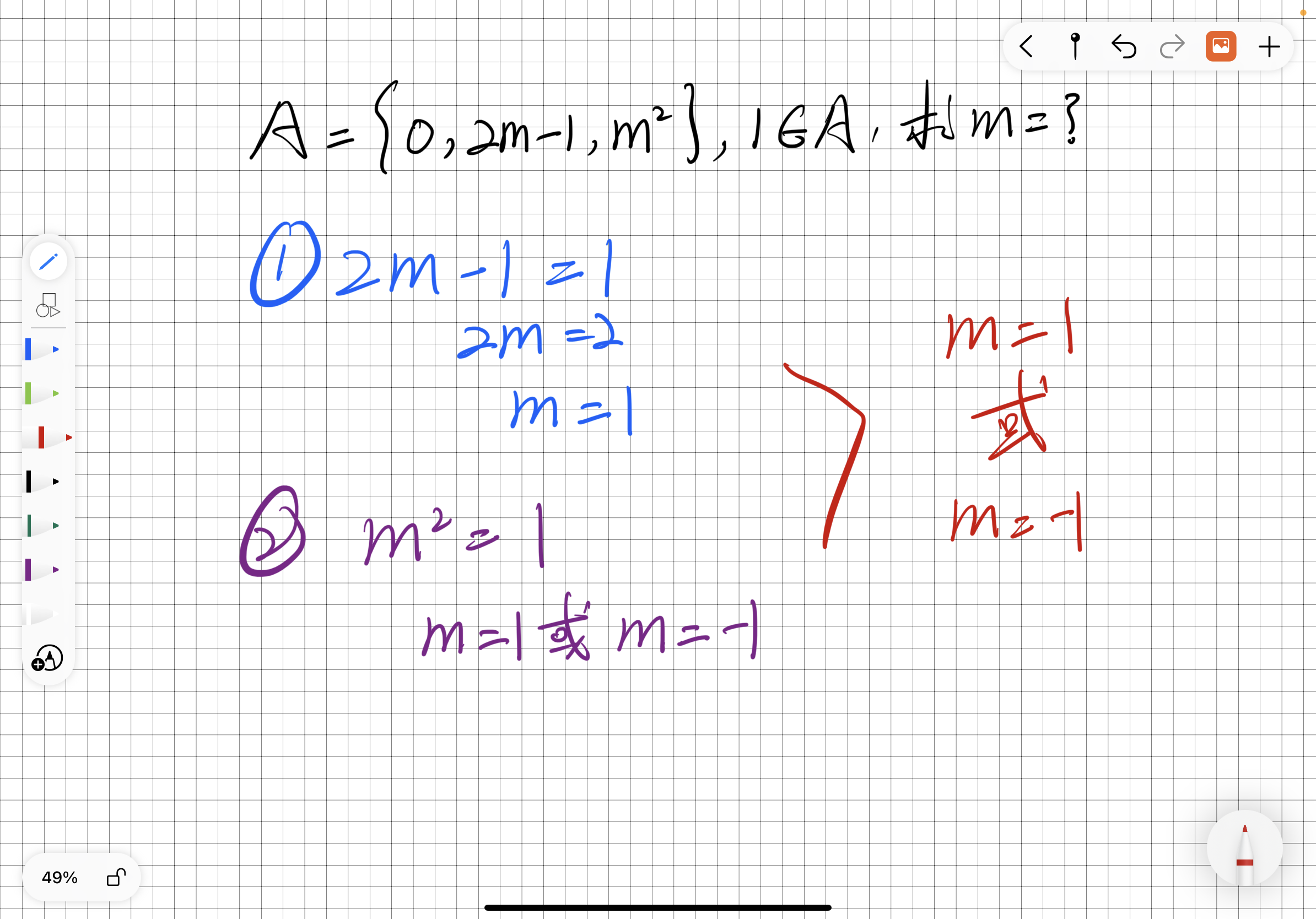
代数互异性（1）【|元素的互异性具体应用，真没那么简单（详解含参方程解集）】关于代数的互异性，同学们十有八九都会忽略，比如图中的集合，求m的值，很多同学的第一反应肯定是2m-1 ， m中肯定有一个是1 。
那么我们来计算一下，如下图，求得第一个式子为1 ，第二个式子为m=1或者m=-1 ，答案进行一个综合m=1或m=-1 ，这道题就做完了。
如果你真的认为这就完事儿了，那么你真的早就掉坑了，你想到互异性了吗，不信你就把值带回去A集合看一下，是不是元素之间互不相同，如果m=1 ，那么2m=1 ， m=1 ，这下整个集合就出现了两个1 ，因此m=1是不能要的，接下来赶紧看看m=-1是不是也有问题，经过下图计算，集合就变成{0 ， -3 ， 1 ，看来m=-1是没有问题的。
小提示：求出答案以后一定要将结果带到原集合中进行检验，这个步骤也被称为互异性检验。

这种算来算去的求值里，就更加要注意，尤其是越复杂的题目，往往难题的崩塌就在某个简单的计算之中。
代数互异性（2）那么我们把上边的问题变得复杂点，将1属于A变为4m-4属于A ，那么现在的这个m如何进行计算呢？首先计算的方式是一样的，既然4m-4属于A ，那么A中的三个元素肯定就如下图中所示与其相等，我们就需要分三种情况进行讨论。

第一种情况，我们得到m=1
第二种情况，我们得到m=2/3
第三种情况，我们得到唯一解m=2

接下来，我们就该做互异性检验了
我们将m带回原集合，算出原集合中的具体元素即可，由于比较简单，也避免文字啰唆，我们在下图中直接计算出了结果，将第一排重合的结果舍掉，其余的留下来最终得出， m=2/3或m=2 。
总结今天由于是例题，讲的都是元素互异性的具体应用，有一点非常关键，在你算出结果之后，一定要将结果带回原集合中检验互异性，数学科目，失之毫厘，差之千里，同学们学会了吗？今天的课程就到这里结束了，我们下节课讲解《二次方程解集个数》，也是非常重要的小知识，我们下节课见！