把矩阵看作一个算子——从几何角度解释对称矩阵的三个最重要性质

文章图片

文章图片

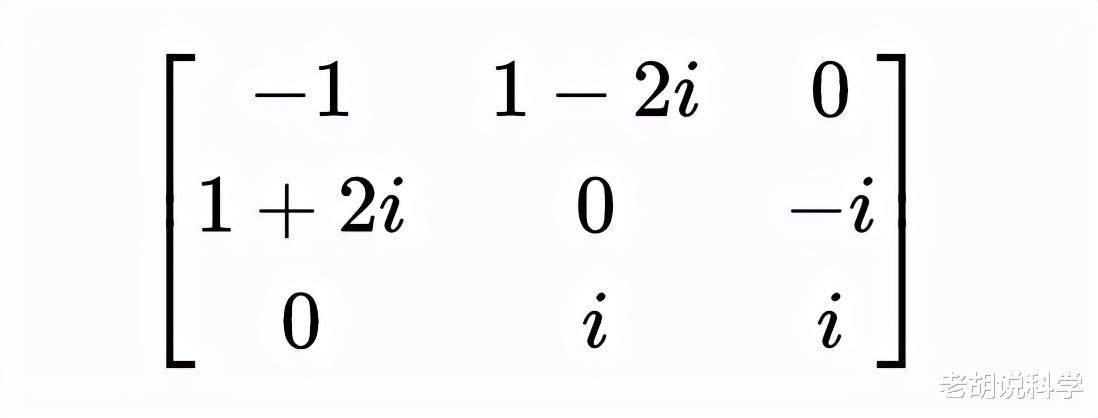
文章图片

文章图片

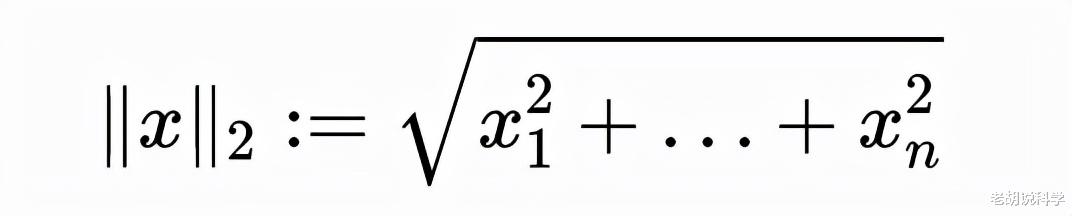
文章图片

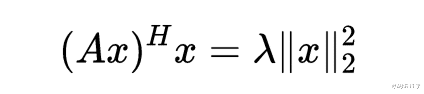
文章图片

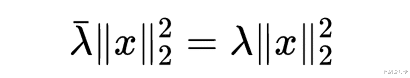
文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

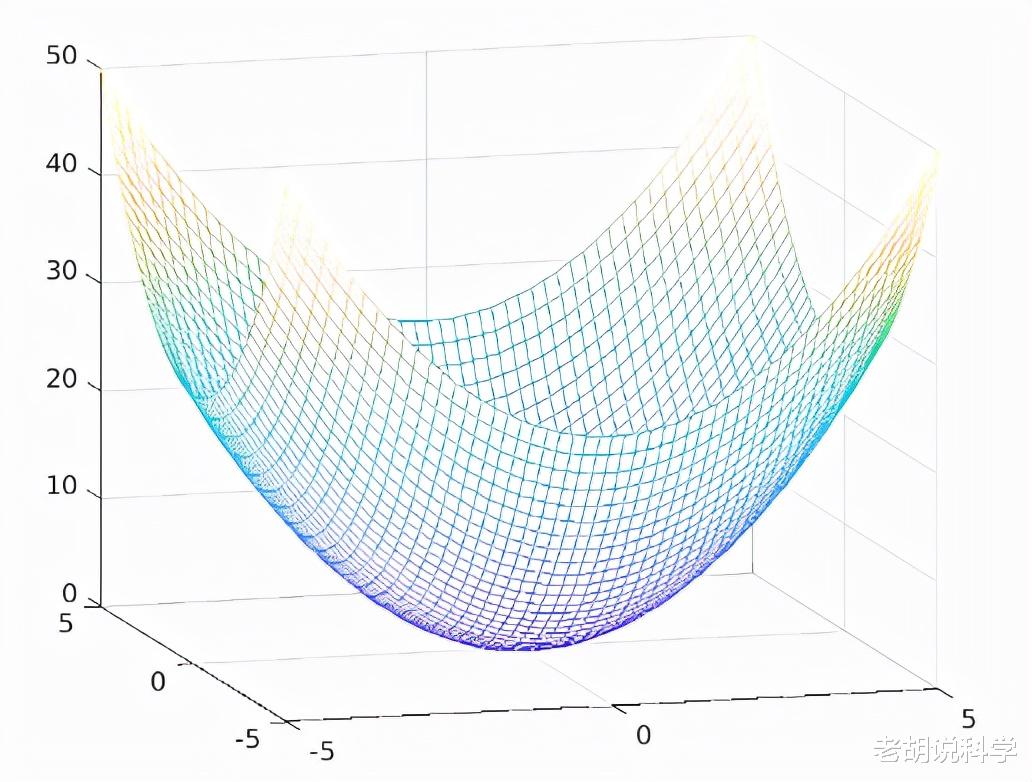
对称矩阵是沿对角线对称的矩阵。它是一个自伴算子（self-adjoint operator）（把矩阵看作是一个算子并研究其性质确实是一件大事）。虽然我们不能直接从对称性中读出几何属性，但我们可以从对称矩阵的特征向量中找到最直观的解释，这将使我们对对称矩阵有更深入的了解。
常见的例子是单位矩阵。一个重要的例子是：

对称矩阵的一个例子

然而，虽然定义简单如斯，但却意义非凡。在这篇文章中，我们将看一看它们的重要属性，直观地解释它们，并介绍其应用。
厄米特矩阵（The Hermitian matrix）是对称矩阵的复扩展，这意味着在厄米特矩阵中，所有元素都满足：
厄米特矩阵的共轭转置与自身相同。因此，它具有对称矩阵所具有的所有性质。

厄米特矩阵的一个例子

在这篇文章中，我主要讨论的是实数情况，即对称矩阵，以使分析变得简单一些，同时在数据科学中，我们遇到的也大都是实矩阵，因为我们要处理现实世界的问题。
对称矩阵的最重要的性质本节将介绍对称矩阵的三个最重要的性质。它们涉及这些矩阵的特征值和特征向量的行为，这是区别对称矩阵和非对称矩阵的基本特征。
性质1. 对称矩阵有实数特征值
这可以很容易地用代数法证明（正式的、直接的证明，而不是归纳法、矛盾法等）。首先，快速回顾一下特征值和特征向量。