在物理学家的干涉下，量子们快乐地玩耍

文章图片

江苏激光联盟导读：
《量子》杂志发布量子双缝实验新成果。

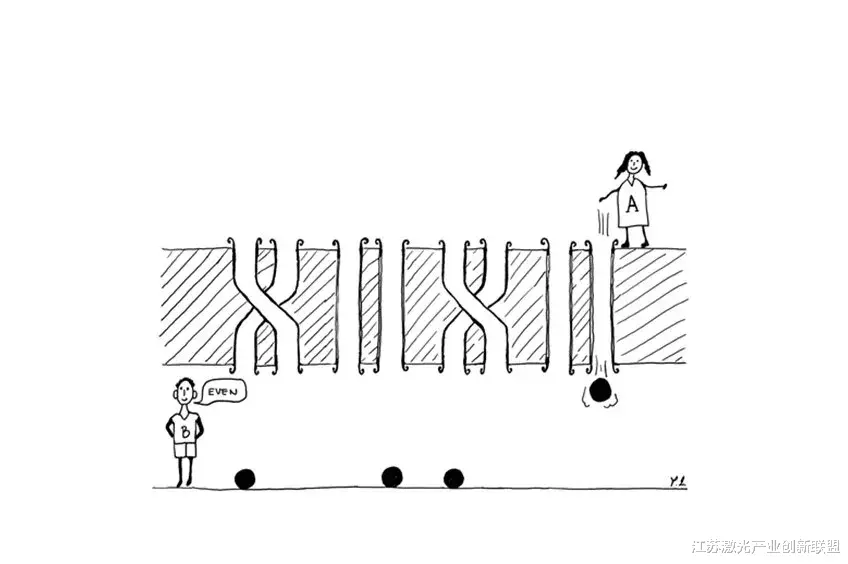
图中展示了最简单的平价游戏例子。 Alice (A)向Bob (B)弹一定数量的弹珠，目的是了解扭曲的管子的数量是偶数还是奇数。玩家需要四个普通的古典弹珠来完成任务。相比之下，两个量子弹珠就足够了。来源：? Borivoje Daki?

二十世纪著名物理学家、诺贝尔奖得主Richard Feynman曾说了这样一句名言：“双缝实验绝对不可能用任何经典的方法来解释，它是量子力学的核心。事实上，它包含着唯一的奥秘。 ”

量子像孩子一样调皮

双缝实验图源：网络
事实上，在这个实验中，一个量子粒子表现得好像它同时处于两个不同的位置，并显示出类似于聚合波的现象，例如干涉。然而，后来有人注意到，多缝实验表明，量子粒子的离域程度有其局限性，在某种意义上，量子粒子不能同时在两个以上的位置离域。这种限制造成了一个至今尚未完全解决的难题。维也纳大学和iqqi -Vienna(奥地利科学院)的研究人员已经在理解这个问题上迈出了重要的一步，他们从信息理论游戏的角度重新制定了干扰实验。他们的分析最近发表在《量子》杂志上，提供了一种直观的方式来思考干涉现象及其局限性，从而为解决上述难题铺平了道路。
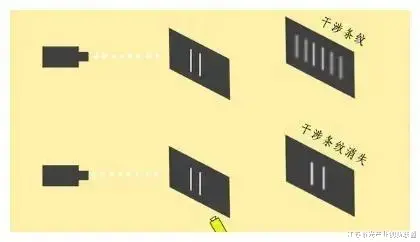
量子力学最显著的特征之一是叠加原理。这个原理可以通过双缝实验来很容易地说明，这个实验涉及一个粒子通过一个有两个缝的板。根据我们日常的直觉，人们可能会认为粒子总是要么通过一条缝，要么通过另一条缝。然而，量子力学暗示，在某种意义上，粒子可以同时通过两个狭缝，也就是说，它可以同时处于两个位置的叠加。这种可能性是量子干涉现象的基础，即量子粒子所表现出的惊人的波状行为。现在，有没有一种方法可以量化量子粒子去局域化的程度?量子理论允许粒子同时通过两条以上的路径吗?为了理解这些问题，物理学家们分析了“多缝实验” ，它与双缝实验的区别只是在缝的数量上:例如，三缝实验涉及一个粒子通过三个缝被发送。
有人可能会认为，如果一个量子粒子可以同时通过两个狭缝，那么它也应该能够同时通过三个、四个或任意数量的狭缝。令人惊讶的是，人们立即注意到，在多缝实验中得到的任何图形都可以用粒子总是最多同时通过两个缝来解释。即使从数学上完全理解了这一特征，以下问题仍然没有得到解答:双缝实验和多缝实验之间明显的不对称是否有物理原因?这种对量子粒子的“非定域”的武断限制的基础是什么?

在三种模拟光纤的实验中，干涉图样(上)和计算相关性(下) 。数据位“000”和“111”是由光波噪声中的负相关和正相关导出的，可见的光斑和黑点。

维也纳大学和奥地利科学院的研究人员Sebastian Horvat和Borivoje Daki?在他们最近的工作中，通过利用信息论解决这一问题，在理解这一问题上迈出了重要的一步。也就是说，他们用“奇偶博弈”重新表述了干涉现象和多缝实验，最简单的例子如图1所示。这个游戏有两个玩家， Alice和Bob ，他们被一堵用四对管子穿穿的墙隔开。每对管子可以是直的，也可以是双绞的，而双绞的数量对Alice和Bob都是未知的。此外， Alice有一定数量的弹珠可以穿过管子把弹珠弹给Bob 。玩家可以用这些弹珠来了解管子的结构。
游戏的目的是让玩家合作，通过使用尽可能少的弹珠，找出缠绕成对的总数是偶数还是奇数。现在，假设Alice把一个弹珠扔进了其中一个管子（如第二个管子）。然后， Bob就可以简单地判断出第一对管子是直的还是扭曲的，只要检查弹珠是穿过第二根管子还是穿过第一根管子就可以了。类似地，如果Alice有四颗弹珠，她可以将每一颗弹珠弹过每一颗弹珠的右管(如图1所示) 。然后Bob可以直接推断双绞线的数量，从而判断这个数字是偶数还是奇数，从而赢得游戏。然而，如果两根管的数量超过了Alice所拥有的弹珠的数量，那么这个游戏就不可能赢，因为总会有至少一根管，而Bob无法收集到任何信息。因此，为了赢得游戏，玩家需要使用尽可能多的弹珠。

在物理学家的干涉下，量子们快乐地玩耍

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)