文章图片
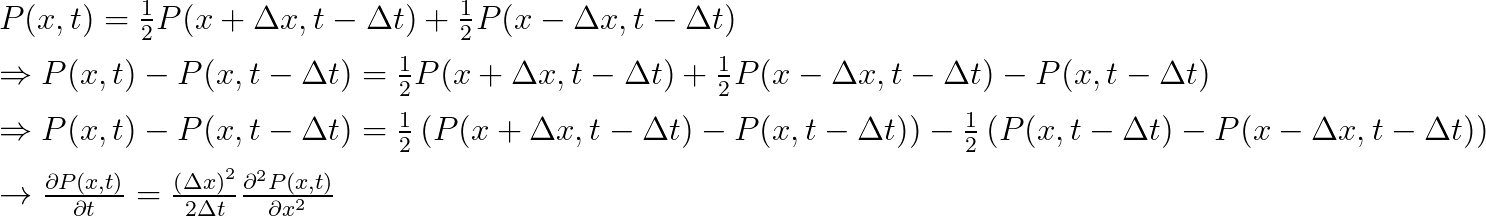
文章图片
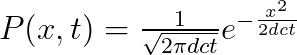
文章图片
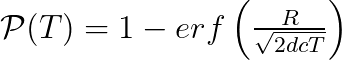
文章图片
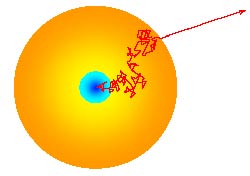
有一个流行的说法:光子从太阳核心到太阳表面需要数万年的时间 , 但从太阳表面到地球只需要8分钟 。 在这个说法背后 , 是光子在太阳内部的布朗运动 , 在数学上我们可以用随机游走模型进行计算 。
核聚变产生的光子会被其它原子重新吸收并释放到另一个方向 , 在这期间它平均移动了一个距离d;给定d和光速c , 我们可以计算出平均时间步长和空间步长;太阳的尺寸可以用步长进行衡量 , 最后 , 光子到达太阳表面的平均时间就能被计算出来 。
开始数学计算
如果一个粒子平均每Δt时间内以随机方向(左右各50/50)移动一个Δx的距离 , 那么该粒子在特定时间特定地点的概率P(xt)满足下列方程:
接下来 , 我们在等式的两边减去P(x , t-Δt) , 并巧妙构造出微分方程 。
在太阳这个例子中 , 平均自由程Δx=d , 这意味着在光速下 , Δt = d/c , 代入上面的微分方程 ,
我们可以解
我们关心的是时间 , 我们要计算的是在某个时间T , 粒子超出太阳半径R的概率 , 因此我们可以dx进行积分 。 由于对称性 , 只需要关心一边的情况就够了 , 因此x的范围从R到正无穷 , 并且式子还要乘以2 , 得到:
对于这么复杂的方程 , 我们可以用高斯误差函数进行重新表达:
之所以这么做 , 是因为数学太难了 , 前人有研究结果我们就直接套用 , 可以省下很多计算时间 。
现在 , 我们可以得到 , 当erf()=1/2时 , 光子有50%的概率已经逃脱了太阳 , 此时:
代入R=7×10^8米 , c=3×10^8米/秒 , d=0.0001米 , 我们可以解得T=110万年 。
当然 , 太阳的不同部分有不同的d值 , 这使得严谨的计算变得更加困难 。 考虑到我们对太阳的了解 , 有些人认为真实时间应该在10万年左右 。 此外 , 我们的计算也忽略了很多事实 , 比如把太阳当成一个线段而不是球体 , 还有光子被吸收和释放的时间等 。 因此 , 这更像是一种假设计算 。
【核聚变产生的光要经过数万年才能逃离太阳,这个结果是如何计算的】
推荐阅读
- 简述相对论发展史:从伽利略到引力波
- 除了黑洞还有白洞?爱因斯坦:白洞是黑洞的反演,能穿梭时间
- 50亿光年外,天文学家发现星系一分为二,爱因斯坦又对了?
- 平行宇宙理论是否支持回到过去?——霍金时间派对番外篇 原创
- 4维空间存在?德国数学家已证明,进入4维空间后人会变成什么?
- 杨利伟进入太空后听到敲窗声,16年后真相揭开,庆幸捡回一命
- 我国将造新一代“观天神器”爱因斯坦探针,超强视力可让黑洞现形
- 爱因斯坦称人类只要掌握这种力,即可任意进入更高维度并改天换地?
- 全球化国际教育系列——爱因斯坦
- 如果用上所有的核弹,人类真的可以毁灭地球吗?







