张量|进展 | 求解组合优化问题的“热带”张量网络方法_组合优化|科学|自旋|科普|科技

组合优化问题关心如何找到离散优化问题的最优解，在科学和工程领域有广泛的应用。很多组合优化问题，例如旅行商问题、图染色问题等都是所谓的NP难问题。因此也许并不存在一般性高效率的求解方法。
统计物理中关心的自旋玻璃模型的基态问题也属于NP难的组合优化问题。为此，物理学家和计算机科学家们发明了各种各样的严格的和启发式的方法来寻找系统的基态。此外，当自旋玻璃模型存在简并的基态时，严格地数基态的个数(即计算零点熵)属于更难的一类计数问题。在最近的工作中，中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T03组的刘金国博士（现哈佛大学博士后）和王磊研究员与中科院理论物理研究所张潘研究员合作，提出了一种基于“热带”张量网络的严格求解组合优化问题的最优解和零点熵的方法。
这个工作将张量网络收缩中的加乘运算替换为定义在极大-加法半环上的“热带”代数(Tropical Algebra) 。通过收缩“热带”张量网络，可以直接计算自旋玻璃模型的基态能量和熵。对网络收缩过程求导，可以得到基态自旋构型。结合泛型编程，此方法可以充分利用量子线路模拟器（例如刘金国等前期开发的Yao.jl）、自动微分技术和专用硬件的算力。作者使用此方法研究了二维、三维、Chimera图、随机图上的自旋玻璃模型，以及Potts玻璃模型和最大约束满足等物理和计算机科学中的组合优化问题。在不少情况下“热带”张量网络方法比传统的计算方法算得更快或可以求解更大尺寸的问题。这项进展融合了统计物理、张量网络、机器学习以及量子计算等领域中的概念与方法，为求解组合优化问题提供了一个新工具。
相关研究成果近期发表于物理评论快报[Phys. Rev. Lett. 126, 090506 (2021)] 。论文链接 https://link.aps.org/doi/10.1103/PhysRevLett.126.090506 。开源实现见 https://github.com/TensorBFS/TropicalTensors.jl 。另可参考刘金国博士编写的教学程序https://giggleliu.github.io/notebooks/tropical/tropicaltensornetwork.html 。该工作得到了国家自然科学基金委（11774398）和科技部（2016YFA0300603 ， 2016YFA0302400）的资助。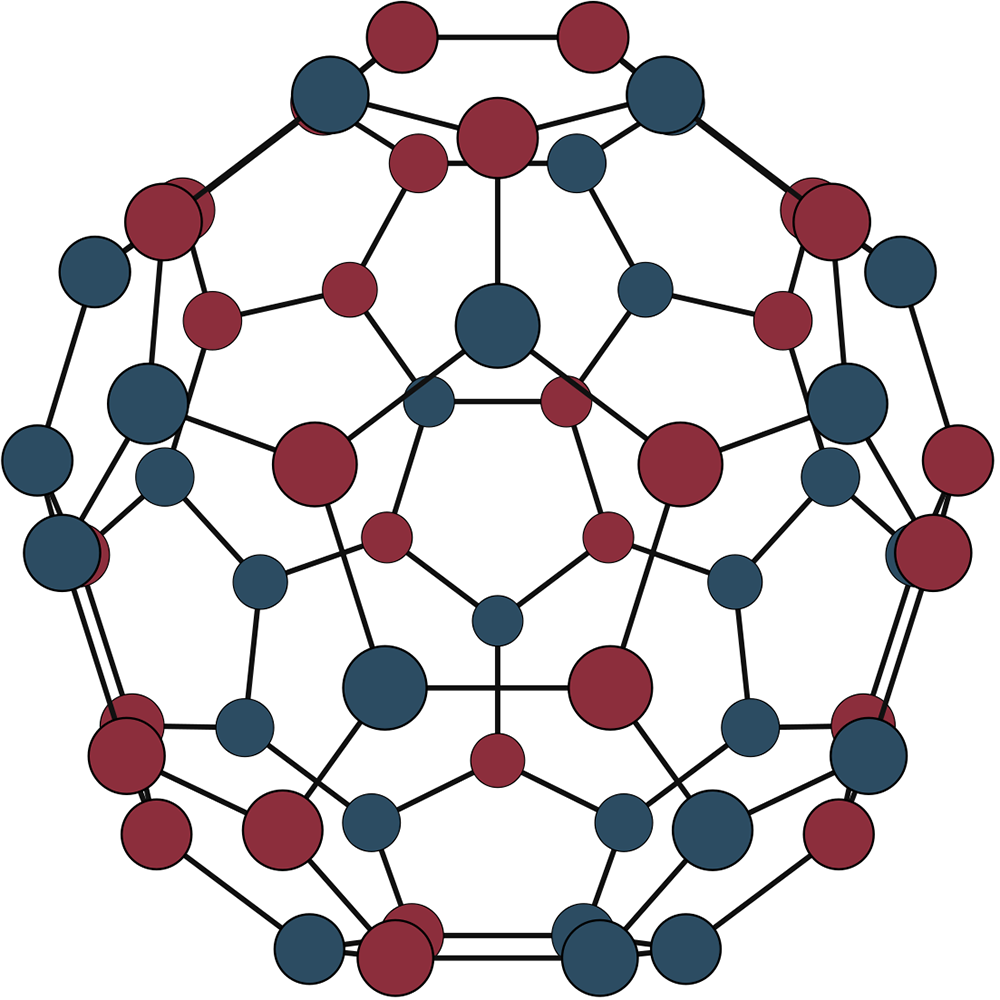

本文图片

C60晶格上反铁磁伊辛模型的基态构型之一【张量|进展 | 求解组合优化问题的“热带”张量网络方法】编辑：yrLewis

张量|进展 | 求解组合优化问题的“热带”张量网络方法

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)