分析|拓端tecdat|Python中的Lasso回归之最小角算法LARS_pyplot|因变量|问题|解决方案|

原文链接：http://tecdat.cn/?p=20379
假设我们期望因变量由潜在协变量子集的线性组合确定。然后， LARS算法提供了一种方法，可用于估计要包含的变量及其系数。
LARS解决方案没有给出矢量结果，而是由一条曲线组成，该曲线表示针对参数矢量L1范数的每个值的解决方案。该算法类似于逐步回归，但不是在每个步骤中都包含变量，而是在与每个变量的相关性与残差相关的方向上增加了估计的参数。
优点： 1.计算速度与逐步回归一样快。
2.它会生成完整的分段线性求解路径，这在交叉验证或类似的模型调整尝试中很有用。
3.如果两个变量与因变量几乎同等相关，则它们的系数应以大致相同的速率增加。该算法因此更加稳定。
4.可以轻松对其进行修改为其他估算模型（例如LASSO）提供解决方案。
5.在p >> n的情况下有效（即，当维数明显大于样本数时）。
缺点： 1.因变量中有任何数量的噪声，并且自变量具有多重共线性，无法确定选定的变量很有可能成为实际的潜在因果变量。这个问题不是LARS独有的，因为它是变量选择方法的普遍问题。但是，由于LARS基于残差的迭代拟合，因此它似乎对噪声的影响特别敏感。
2.由于现实世界中几乎所有高维数据都会偶然地在某些变量上表现出一定程度的共线性，因此LARS具有相关变量的问题可能会限制其在高维数据中的应用。
Python代码：

import matplotlib.pyplot as plt # 绘图
diabetes

查看数据

文章图片

x /= np.sqrt(np.sum((x)**2, axis=0)) # 归一化 x
lars.steps() # 执行的步骤数
est = lars.est() # 返回所有LARS估算值
plt.show()

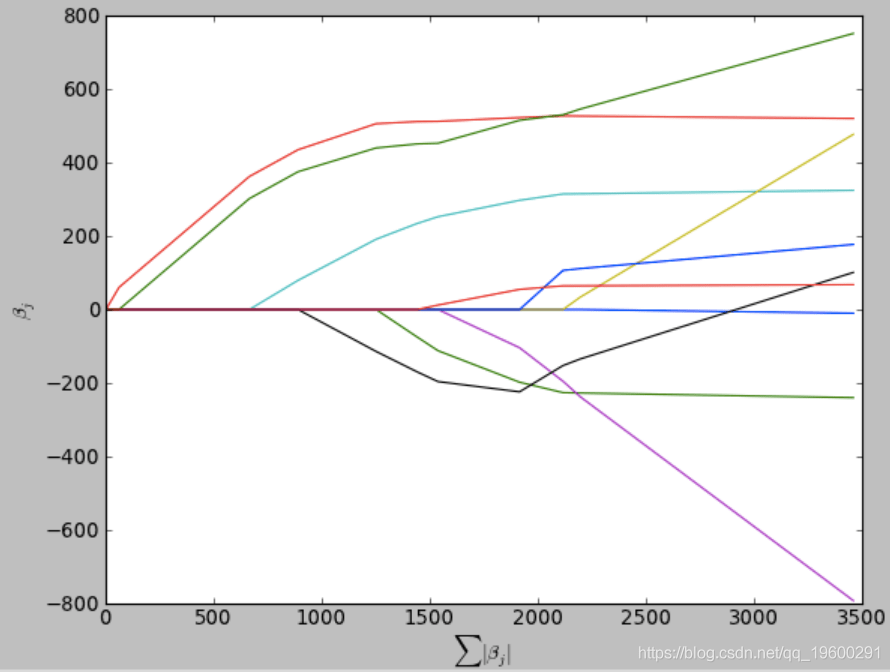
文章图片

文章图片

最受欢迎的见解
1.R语言多元Logistic逻辑回归应用案例
2.面板平滑转移回归(PSTR)分析案例实现
3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）
【分析|拓端tecdat|Python中的Lasso回归之最小角算法LARS】4.R语言泊松Poisson回归模型分析案例
5.R语言回归中的Hosmer-Lemeshow拟合优度检验
6.r语言中对LASSO回归， Ridge岭回归和Elastic Net模型实现
7.在R语言中实现Logistic逻辑回归
8.python用线性回归预测股票价格
9.R语言如何在生存分析与Cox回归中计算IDI ， NRI指标