月球的大小实际上 , 在阿里斯塔克遗存的一本书中提到了有关太阳和月亮的大小以及他们的距离 。 在这本杰出的著作中 , 阿里斯塔克列出了已知最早的对太阳和月亮的相对大小和距离的尝试性计算 。
长期以来 , 人们观察到太阳和月亮在天空中似乎具有相同的大小 , 但太阳比较远 。 这一点是他们从日食中意识到的 , 日食是由月球在离地球一定距离的地方从太阳前面经过引起的 。
此外 , 阿里斯塔克还推断太阳、地球和月球将在月球处于第一或第三季期间 , 三者形成一个直角三角形 。
由于毕达哥拉斯早在几个世纪前就确定了三角形边长的关系 , 阿里斯塔克利用这个三角形估计到太阳的距离是到月球距离的18到20倍 。 他还根据对月食的仔细计时 , 估计月球的大小约为地球的三分之一 。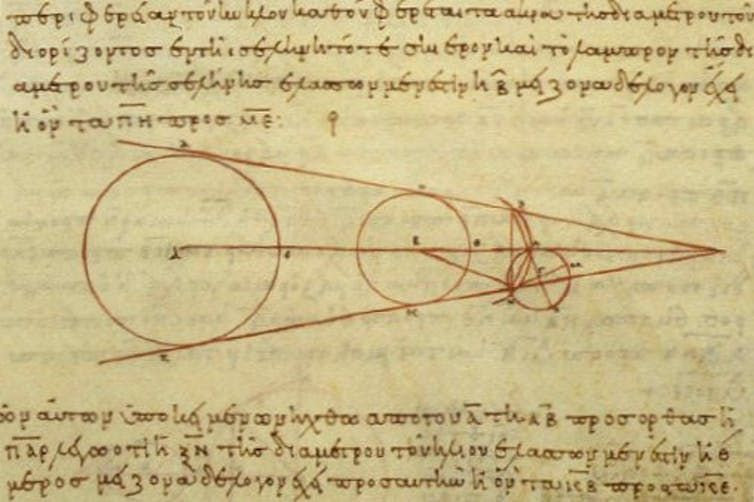
一张10世纪阿里斯塔克的图的复制品 , 显示了他在计算中使用的一些几何图形 。 (图片来源:维基百科 , CC BY-SA)
在当时缺乏精确的望远镜的条件下 , 他估计的与太阳的距离过低(实际比例为390) ,, 但地球与月球的大小比例值却出奇地准确(月球的直径是地球的0.27倍) 。
今天 , 我们通过各种手段准确地知道了月球的大小和距离 , 包括精确的望远镜、雷达观测和阿波罗宇航员留在月球表面的激光反射器 。
3. 地球的周长
埃拉托色尼Eratosthenes(公元前276年至公元前195年)是亚历山大大图书馆的首席图书管理员 , 也是一位敏锐的实验家 。 已知最早地计算地球周长是他众多成就的其中之一 。 毕达哥拉斯一般被认为是最早的球形地球的支持者 , 尽管还不知道其大小 。 埃拉托色尼计算的方法著名而又简单 , 夏至日正午时分在不同维度的地区 , 向地面垂直插入杆子 , 测量其投下影子的不同长度从而进行计算 。
太阳离地球足够远 , 所以无论它的光线到达哪里 , 它们实际上都是平行的 , 这正如阿里斯塔克过去书中所言 。 因此 , 阴影的差异表明了地球表面的弧度 。 埃拉托色尼利用这一点来估算地球的周长约为40000公里 。 这与现代大地测量学(研究地球形状的科学)确定的实际值相差无几 。
后来 , 另一位名叫波西多尼Posidonius的科学家(公元前135年至公元前51年)使用了一种略有不同的方法 , 得出了几乎完全相同的答案 。 波西多尼一生中大部分时间都住在罗德斯岛 。 在那里他观察到亮星Canopus非常接近地平线 。 然而 , 当他在埃及的亚历山大城时 , 他注意到Canopus会上升到地平线以上约7.5度的位置 。
推荐阅读
- 星链|石豪:在太空,马斯克和美国当局是如何作恶的
- 快报|“他,是能成就导师的学生”
- 区块|面向2030:影响数据存储产业的十大应用(下):新兴应用
- 年轻人|人生缺少的不是运气,而是少了这些高质量订阅号
- 生活|气笑了,这APP的年度报告是在嘲讽我吧
- bug|这款小工具让你的Win10用上“Win11亚克力半透明菜单”
- 苏宁|小门店里的暖心事,三位创业者的雪域坚守
- 历史|科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 空间|(科技)科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 生活|数字文旅的精彩生活







