文章图片
文章图片

文章图片

文章图片
然而 , 按照能量守恒定律 , 质量越大的物体 , 达到一定速度时所需要的能量就越多 。 通过洛伦兹变化 , 推导出物体运动“质增效应”公式 , 我们可以看出 , 当以光速运行时 , 物体的运动质量就会变得无穷大 , 所以有质量的物体 , 是永远也达不到光速的 。
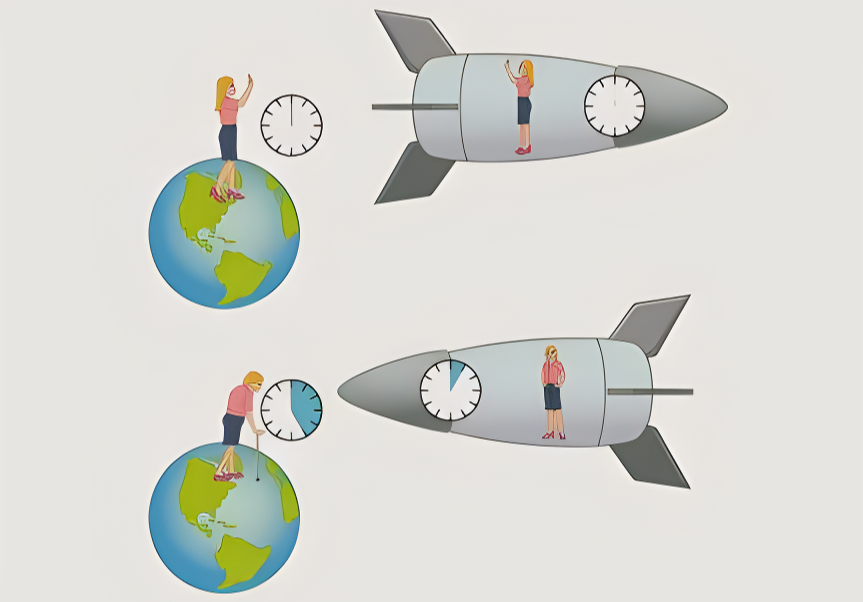
之所以构成光线的光子速度能够达到光速 , 原因就在于光子的静止质量为零 。 而按照狭义相对论 , 同样可以推导出以光速运行下的种种奇妙现象 , 比如“钟慢”效应、“尺缩”效应 。 我们接下来用“钟慢”效应 , 来看看如果乘坐以光速飞行的宇宙飞船 , 1个小时后地球上的人们到底过去了多久 。
说到“钟慢”效应 , 不得不先提一下狭义相对论下的速度“叠加” 。 经典物理学中 , 速度的叠加 , 无非就是同一条直线上的有效速度之和或者是它们之间的差值 。 但狭义相对论中 , 在两个惯性参照系下 , 两个物体的运动合速度 , 与原来两个物体在一条直线上的各自有效速度间 , 存在着这样的对应关系:v=(v1+v2)/(1+v1*v2/c^2) , 通过这个关系式 , 我们可以看出 , 无论原来两个物体速度多快 , 即便是相反方向 , 它们的合速度依然不会超过光速 。
在这个光速不变原理基础上 , 通过推导 , 可以得出高速运动物体 , 能对不同惯性参照系下的空间移动、时间流逝的影响程度 。 以“钟慢”效应为例 , 处于两个惯性参照系下 , 两个物体所处的时间流逝对应关系为:T’=T/√(1-v^2/c^2) 。
式中 , v为高速飞船速度 , c为光速 , T’为地面经历时间 , T为飞船经历时间 。
如果飞船的运动速度越快 , 那么在飞船所在的惯性参照系内 , 时间的流逝速度虽然正常 , 但对于地面来说 , 属于未发生明显位移的惯性参照系 , 从地面看 , 飞船上的时间过得越来越慢 。
这里面存在着一个疑问 , 那就是运动是相互的 , 从地球上看飞船以高速运行 , 飞船上的时间过得很慢 , 那么从飞船上看地球 , 也同样以高速远离 , 是不是时间过得同样慢呢?如果一样的话 , 就不会存在“钟慢”效应了 , 大家毕竟都慢嘛 。
这里还得提一下 , 狭义相对论的成立条件 , 即必须是在惯性参照系内 , 两个不同参照系内的物体运动 , 必须处于匀速直线运动或者静止的状态 , 如果有一方发生变速(速度大小或者方向改变) , 那么狭义相对论就会不再适用 。 因此 , 如果光速飞船离开地球后 , 一路向前匀速前进不再返回 , 那么无论从哪个参照系看 , 两者的时间流逝速度 , 都相互独立且不受彼此影响 , 不发生任何信息交流 , 也没有什么时间流逝的对比产生 。
显然这不是我们要的结果 , 我们就是想通过超高速运动下两个物体的运动 , 来衡量彼此的“时间差” 。 为了不产生“双生子悖论” , 科学家们认为 , 哪一方先打破惯性参照系 , 就以这一方为基础 , 来推算另外一方的时间流逝速度 。
如果人们乘坐光速飞船飞出一小时再回来 , 显然地球的运动状态没有什么改变 , 那么打破“规律”的自然是飞船 。 按照飞船的速度 , 套用上面的“钟慢”公式 , 我们就能看出地球上的人类 , 所经历的时间流逝速度 , 要大于飞船的时间流逝速度 。
这里 , 我们假设飞船从静止到加速、到接近光速的“过渡时间无限小 , 同样飞船折返瞬间以及再次加速的时间也无限小 , 而且飞船上的人们也能承受住这样的超高加速度 , 我们看一下以亚光速飞行1小时 , 地球上过去了多长时间 。
推荐阅读
- 简述相对论发展史:从伽利略到引力波
- 50亿光年外,天文学家发现星系一分为二,爱因斯坦又对了?
- 这项激光束稳定性的新纪录有助于解决相对论与量子物理不相容性
- 琥珀蜜蜡的。前世今生!
- 隐藏在爱因斯坦相对论里的秘密,我们是否可以让时光倒流?
- 目前已知发现最大的星系,直径400万光年,相当于银河系的25倍
- 过去、现在和未来根本不存在?它们在同一时间块,同时发生(上)
- 激光助力动物的星空旅行
- 物理学中最重要、最美丽的五个基本方程,“导致”很多伟大的发现







