临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘( 二 )

2021-06-03

文章插图

图7：三种不同温度下固体中磁动量的模式

为什么要研究临界现象？关键现象之所以特别吸引人，主要有三个原因：

物理学家还没有完全理解潜在的微观现象
不同的物理系统在接近临界点时表现出非常相似的行为。一个著名的例子是铁磁体和简单流体在接近临界点时的相似性。事实上，对于几组看似不同的系统，临界点指数的数值是相等的。
根据斯坦利的说法，第三个原因是敬畏。他说道:“我们想知道，当我们接近临界温度时，自旋‘知道’怎么会突然对齐。自旋是如何在整个系统中如此广泛地传播它们的相关性的？

配分函数例如，为了研究铁磁体在某温度T时的热平衡性质，原则上我们应该写出它的配分函数。系统的配分函数Z描述了系统处于（热力学）平衡时的统计特性，它是用系统的哈密顿量H来表示的。系统的大部分热力学变量，包括总能和自由能、熵、压力、磁化等，都可以写成配分函数（或其导数）的形式。
配分函数为：

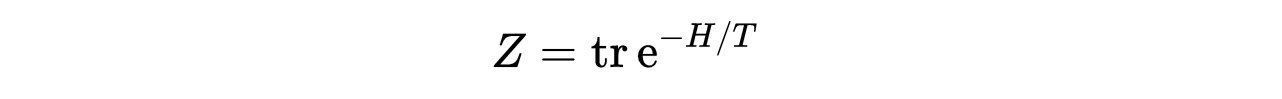
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式2：配分函数有温度T和微观哈密顿量H。

H是微观哈密顿量。我们也可以把Z写成：

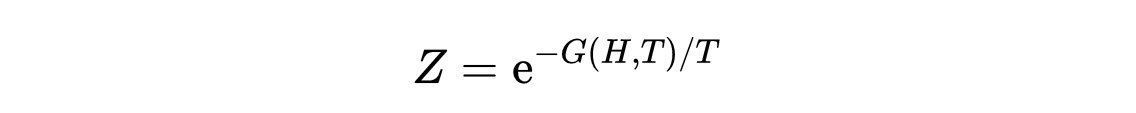
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式3：用自由能G表示的配分函数。

G是吉布斯自由能。后者很重要，因为它有助于识别系统的平衡态。这是因为如果我们让系统保持恒定的温度和压强，当系统处于平衡状态时，吉布斯势最小。
对于非零温度，Z似乎是T的平滑函数，除了临界温度下的非解析行为。
金兹堡—朗道理论（Ginzburg–Landau theory）然而，在大多数复杂系统的情况下，Z不能计算，因此不能使用微观哈密顿量来分析。
这两个著名苏联物理学家列夫·郎道（ Lev Landau）和维塔利金兹堡（ Vitaly Ginzburg）认为，另一种用磁化强度来表示自由能G的方法是考虑G对M的对称性。磁化强度通常被称为序参数。

临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

图8：列夫·郎道（ Lev Landau）和维塔利金兹堡（ Vitaly Ginzburg）

M在临界温度以下消失的数学形式在实验上已知为：

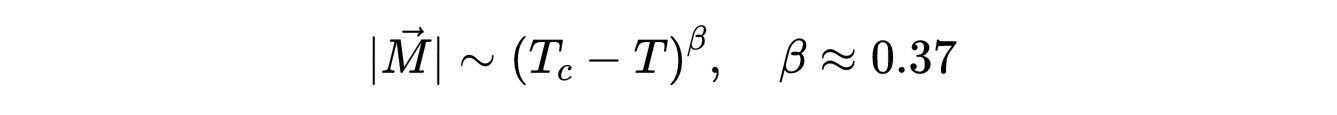
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式4：M消失的数学形式。

临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

图9：自发磁化与大小的关系。曲线是铁(x)，镍(o)，钴(A)和磁铁矿(+)

例如，如果M在x中是常数，旋转不变性将限制自由能G为：

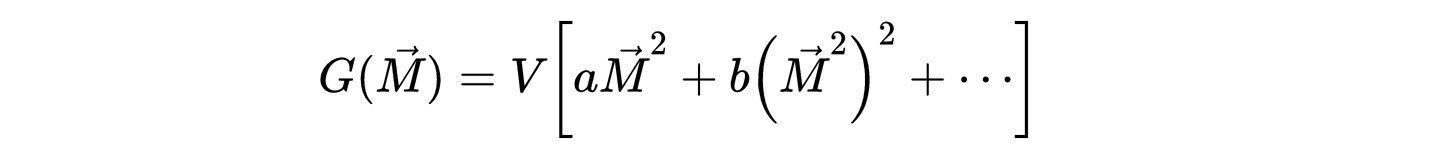
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式5：体积V的旋转不变系统的吉布斯自由能G，用磁化强度M表示。

前因子a，b是未知的，但我们假设它们是温度T的光滑、行为良好的函数（没有奇点或不连续）。假设，根据朗道和金兹堡的理论，a在某个临界温度下消失，很自然地，在接近这个温度时，

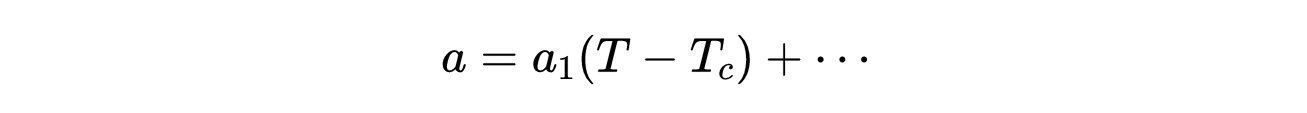
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式6：前因子a的温度依赖性。

打破连续的对称性如何计算一个函数的最小值，如G(M)？考虑Tue的情况，M有两个维度：

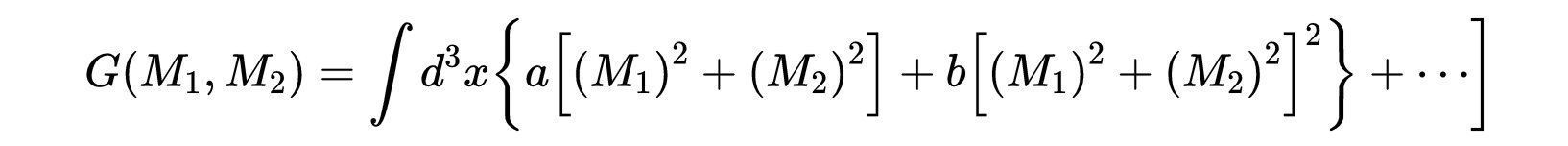
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式7：二维系统的吉布斯自由能G。

最小值发生在，例如：

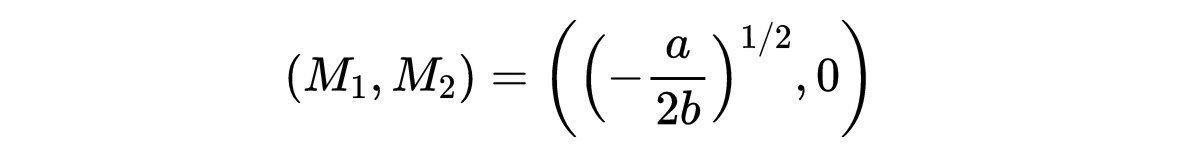
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式8：二维系统吉布斯自由能G的无穷小之一。

其中，第二个分量可以等于以下所示的势能的圆形基数上的任何值（M_2=0只是一个方便的选择）。

临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

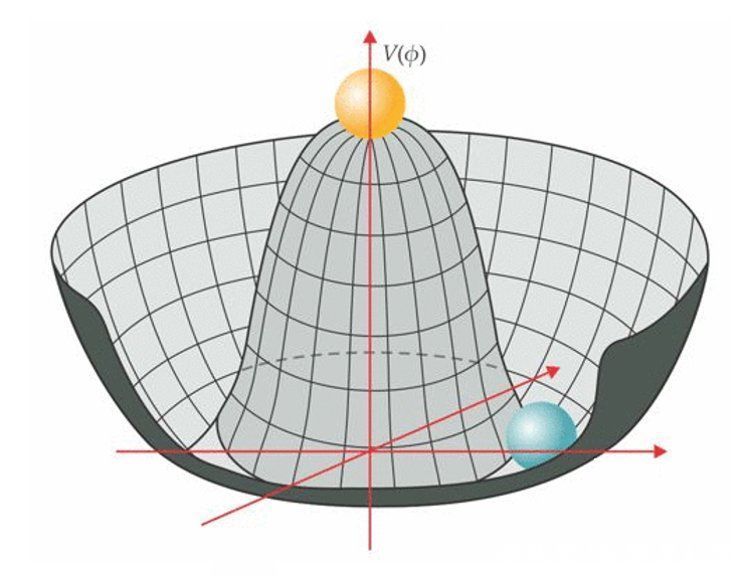
图10：著名的酒瓶底势能

在临界温度以上的温度，G的最小值出现在M=0，但对于低于临界温度的温度，有新的最小值（从上面推导）：

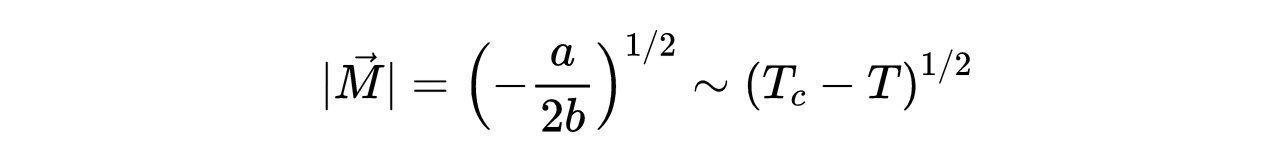
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式9：临界温度以下的最小值。

我们看到旋转对称性自发地打破，出现了非解析性。这是二阶相变的一个例子，这是一种临界现象。
这个G太简单了，我们必须考虑M. Landau和Ginzburg提出的以下归纳：

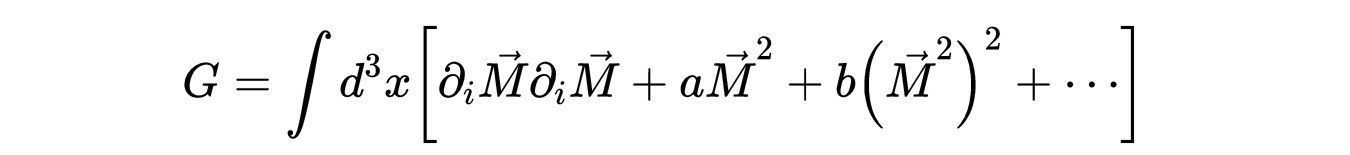
临界点物理临界现象——神秘且微妙的物理世界，多尺度系统的迷人奥秘

文章插图

式10：空间变化磁化的吉布斯自由能G。

我们可以重新缩放M使第一项的系数等于1。

推荐阅读

上一篇：风云四号b星解码风云四号B星：“风云力量”诞生记B星不是“复制”那么简单

下一篇：美国国家航空航天局美航天局宣布将执行两项探索金星的任务