临界点 物理临界现象——神秘且微妙的物理世界,多尺度系统的迷人奥秘( 三 )
在外磁场存在且高于临界温度时,G变成: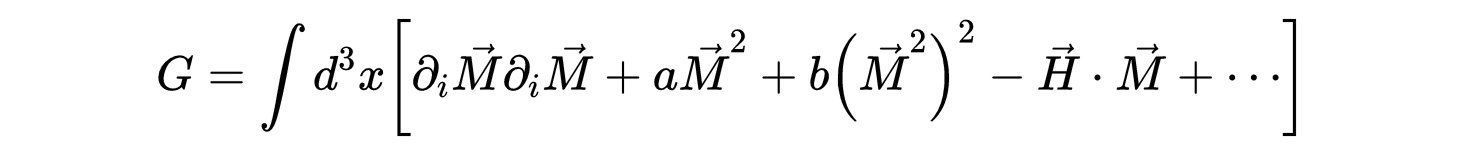
文章插图
- 式11:在外磁场H存在下,空间磁化强度变化的吉布斯自由能G。
对于小M,最小化G得到以下微分方程:

文章插图
- 式12:对小M极小化G得到的微分方程。

文章插图
- 式13:式12的解。
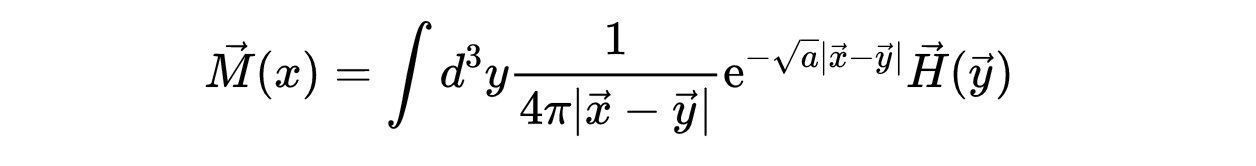
文章插图
- 对k积分后得到式13。
在这里,相关函数的概念很重要。相关函数测量系统中的顺序,不同位置的微观变量如何相互联系,以及它们如何平均(跨越空间和时间)相互变化。在我们的例子中是:
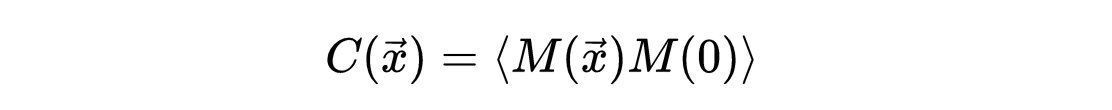
文章插图
- 式15:相关函数。
衰减公式如下:
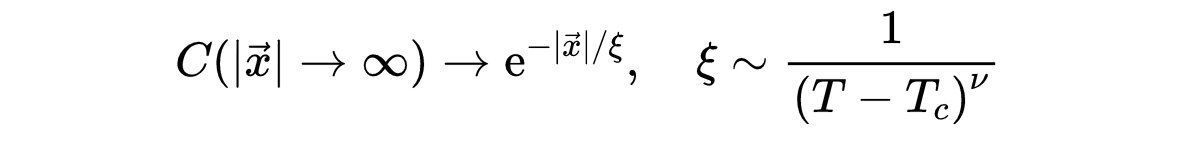
文章插图
- 式16:当T接近临界温度时,C(x)的衰减:
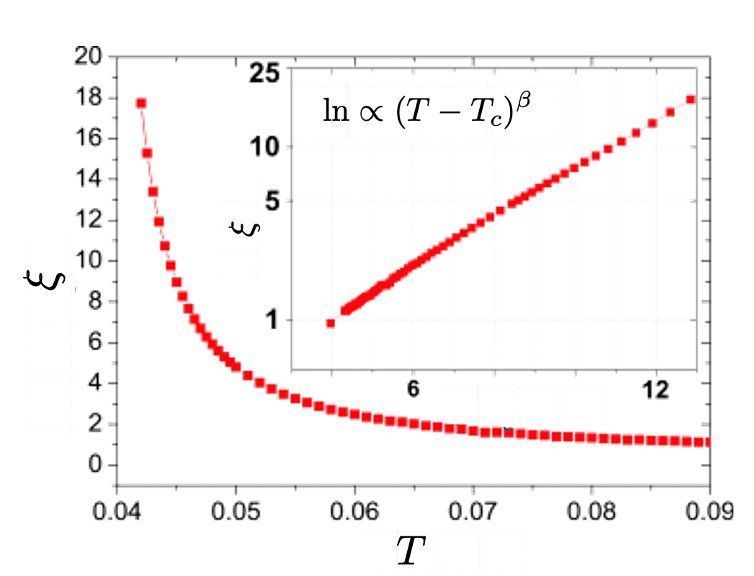
文章插图
- 图11:相关长度随温度变化而发散的实验(临界温度设为1)
使用Landau-Ginzburg理论进行计算,我们发现:

文章插图
- 式17:相关长度和指数ν。
临界指数,标度定律和通用性诸如ν和β等临界指数定义了许多物理量(包括热容、磁化率等)在临界点处的奇点的性质。
但为什么关键指数如此重要?这些指数的组合给出了标度定律,这是一种普适性。实验发现,一些具有完全不同临界温度的系统具有相同的标度指数,而后者是临界指数的组合。
例如,使用我们在上面发现的临界指数,我们得到了所谓的费舍尔标度:
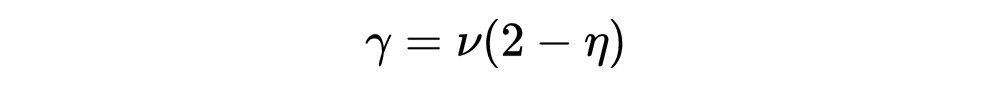
文章插图
- 式18:费舍尔标度,通用指数之一。
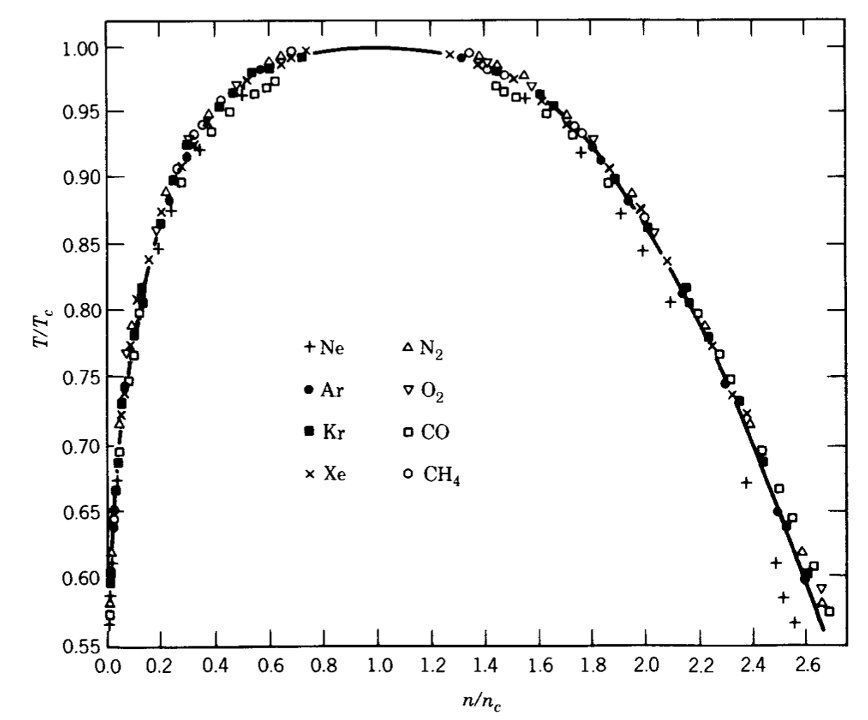
文章插图
- 图12:不同物质在气液共存时温度T和临界温度与降低密度之比
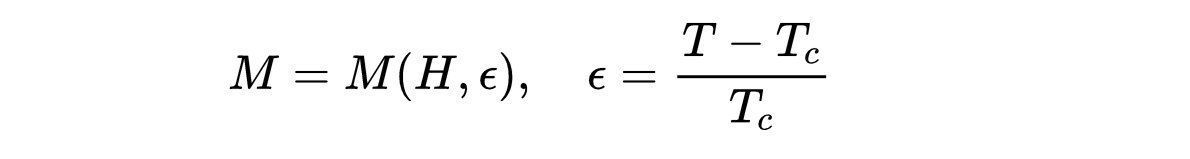
文章插图
- 式19:M对H和还原温度的依赖关系。

文章插图
在临界状态下发现的另一个有趣的性质是通用性。上面的图13是一个例子:由于五种材料具有相同的指数和标度函数,它们属于相同的普适类。
利用重正化群的概念可以得到一个更完整的临界现象理论。
想了解更多精彩内容,快来关注老胡说科学
推荐阅读
- 为什么历史上很多物理学家化学家都终身单身呢
- 固体物理中为什么色散关系Ek是k的周期函数
- 高考不选物理会怎么样 有什么后果
- 初中物理四大学习方法
- 为什么物理版块的民科选手这么多
- 为什么经典物理学时代没有人研究时间
- 怎样学好初中物理?
- 如何评价北京大学物理化学学系刘海超教授
- 初中物理教学问题解决案例分析
- 初中物理该如何学好







