科学家推导高斯磁定律，它是如何否定磁单极的存在的？布莱克本流浪者

文章图片

文章图片

文章图片

文章图片

文章图片
【科学家|推导高斯磁定律，它是如何否定磁单极的存在的？】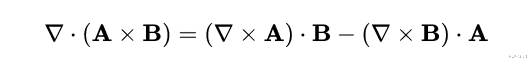

文章图片

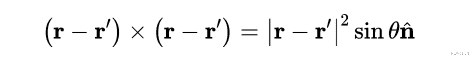
文章图片

文章图片

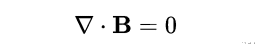
文章图片

麦克斯韦方程以一种相当优雅和数学上紧凑的方式描述了电和磁的相互作用。在这些方程中，高斯的磁定律对于理解电磁波和导电介质之间的相互作用极为重要。但是，这个定律往往被写成简单的形式：

式1

它否认了自然界中磁单极的存在。当涉及到电荷时，我们通常可以认为它们是正的或负的。在这个意义上，当我们把某一空间的所有电荷加起来时，最后总是可以得到一个净电荷或者是零（中性电荷）。磁学的情况则不然。磁铁总是有两个极，北极和南极。即使把一块条形磁铁切成两半：也不会得到两个 \"单极\" 。相反，你会得到两个较小的条形磁铁，每个都有自己的南北两极。因此，当你试图测量通过任何表面的净磁通量时，总是得到零：这意味着不可能存在磁单极，否则磁通量就会是零以外的数值。
尽管这个小方程很重要，但物理学和工程学的学生往往不知道这个方程是如何形成的，或者说它在数学上是如何实现的。在这篇文章中，我将向你介绍得出这一不可思议结果的步骤。
毕奥-萨伐尔定律（The Biot-Savart law）为了开始讨论如何得出公式（1），我们必须首先了解磁场是如何形成的。从几个世纪前的一个小经验观察开始：所有的磁场都是移动电荷的结果。在这个意义上，物体中的每一个原子都拥有自己的磁场，这是由于电子围绕其原子核的运动造成的，但其方向随着时间的推移变化得非常快。
为了充分解释材料中的磁性现象，我们需要研究统计力学（这已经超出了本文的范围）。现在，我们将专注于宏观尺度的磁场。让我们从一个基本的观察开始：任何电流I = dq/dt都是由电子沿着导电材料的运动产生的。如果我们抓起一根宽度可以忽略不计的电线，并以任意的方式在空间中形成一个围绕中心参考点（例如原点）的环形，那么电流I将总是流向一个方向：电线本身的切线方向。然后，让我们定义一个无限小的导线元素dl ，在每一点上都以切线为方向。根据实验证据，运动的电流会产生一个垂直于其运动方向的磁场（因此有一个叫作右手规则的东西）。考虑到这一事实，以及电流引起的磁场强度的经验公式I：

式2

其中r是与电流源（导线）的距离。我们现在通过考虑导线dl的每个元素的贡献来建立一个总磁场。为此，我们考虑到每一点的磁场方向，这是由导线的切向分量和位置矢量之间的叉积给出的。
其中
是沿r-r'指向的单位矢量。这里， r是相对于坐标系的位移矢量，而r'是导线上每一点的无限小元素dl的位置。最后，把所有这些表达式放在一起，可以得到：