时空可数吗？证明时空的可数性，揭示一个深层次的宇宙问题

文章图片

文章图片

文章图片

文章图片

文章图片

文章图片

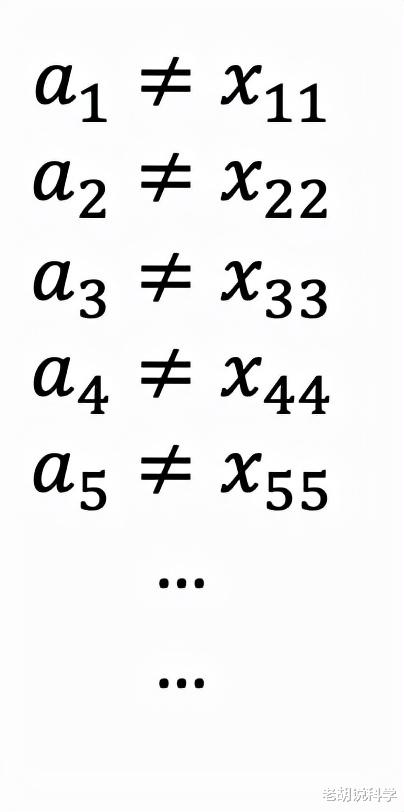
文章图片

我们都熟悉时空的概念，它是简单的三维空间（X、Y、Z）和一个时间维度。在视觉上，一个点可以像下面这样在时空中移动，这被称为参考系。

一个在时空中移动的参考系。

所有这些参考系的合并创造了空间，而任何导致时间移动的因素都使这些参考系在时间中移动。空间和时间是不分开的。你移动得越快，相对于其他静止的人来说，你的时间就越慢。此外，当在一个方向上移动时，那么你就在那个方向上收缩了！这是很重要的。当空间收缩时，时间就会变慢来补偿它。我们想说明的是，时空是不可数的。让我们看看如何说明。
数字?不可数是什么意思？为此，我们必须回到数字上来。
自然数包括数字1、2、3、4、......
整数包括数字... -2 -1 0 1 2 ...
有理数包括数字2/3 ， 6/8 ， 1/2 ，等等。
实数包括数轴上的每一个数字。

自然数N、整数Z、有理数Q和实数R的嵌套。

函数?现在我们有了数字，让我们来看看函数。函数是一种虚构的机器，它从一个集合或空间中获取一些东西，并将其转换为另一个集合或空间中的其他东西。

一个任意的函数。

我们要看的主要有三种类型的函数：单射式（(one-to-one），满射式（onto），以及双射式（one-to-one & onto）。单射是指A中的每个元素只映射到B中的一个元素一次；满射意味着A映射到B的全部；双射意味着A映射到B的全部， A中的每个元素只映射到B中的一个元素一次。从视觉上看，它看起来如下所示：
如果两个集合有相同数量的元素，那么这两个集合之间就会有一个双射的映射。例如，请看下面这张可爱的图片。左边有3只狗，右边有3只猫。如果我们把一只狗和每只猫只映射一次，就得到一个一对一的函数。此外，我们已经涵盖了所有三只猫，因此这个函数是满射的。由于它既是一一对应的，又是满射的，所以它是双射的。这使得我们可以提出以下命题。
命题：当且仅当两个集合之间存在双射，则这两个集合具有相同数量的元素(即相等的基数) 。我们记得这是一个“当且仅当”的命题，这意味着如果第一部分是真的，那么第二部分也是真的(反之亦然) 。如果两个集合具有相等的基数，那么这两个集合之间就存在一个双射。
可数性?有了这些，我们就具备了证明时空不可数所需的一切。首先，我们必须定义可数性是什么意思。假设有一些任意的集合。让我们称它为S（想象一个标有S的空圆，里面什么都没有）。
集合， S ，是：
有限集，如果它是空的，或者具有有限个数的元素。
无限集：如果它不是有限集。
此外，集合， S ，是：
可数集，如果S具有与自然数相同的基数或数字元素。
可列集，如果它是有限的或可数集。
不可数集，如果它不是可数集。
无穷大和可数性并不相互排斥，因为自然数可以达到无穷大。一个例子将有助于说明问题。让我们看看集合S ，这次我们用东西填满它。这个集合里有多少个橙子？
这个橙子集合是可数的。换句话说，我们可能做了以下的事情：
它看起来非常相似，我们只是给每个橙子分配了一个自然数。你会注意到的是，这是自然数和橙子之间的双射。因此，如果自然数和任何任意集合之间存在双射关系，那么这个任意集合就是可数的。这就是我们说某物是否可数的意思。