
文章图片

文章图片

文章图片
【在不违背物理定律的情况下,如何比光速飞船更快到达目的地?】未来的人类一定会步入星际文明时代 , 从最开始的太阳系、再到银河系 , 无限的宇宙才是人类的天地 。 不过想要完成星际旅行 , 就必须解决一个问题——速度 。 宇宙实在太大 , 单单太阳系的直径就接近1
然而 , 伟大的物理学家爱因斯坦告诉我们 , 我们是无法超过光速的 , 想要在短时间内到达数
光速无法超越我们都知道 , 光在真空中传播的速度为299792458米/秒(简称为“c”) 。 只有达到或者超过这个速度 , 我们才能在三维世界里以最短的时间到达想到的地方 。 但在上个世纪 , 爱因斯坦提出了著名的质能方程E=mc2(E=能量 , m=质量 , c=光速) 。
从这个公式里我们可以看出 , 一个物体想要到达光速 , 就需要足够的动能(E) 。 根据质能方程的解释 , 动能越大(E) , 物体运动时的质量(m)就会大于相对静止时的质量 , 这样才能维持质能方程 。
我们以九头蛇70mm火箭弹为例 , 发射的导弹速度为2.7马赫(3308.4公里/小时) , 此时 , 发射出去的炮弹 , 质量就会增加0.00000000004克左右 。 当然了 , 这点质量的增加并不会影响太多的 。
但是当物体的速度越来越快时 , 质量就会呈几何系数增加 , 当物体达到90%的光速时 , 质量就会是静止时的两倍 。 越接近光速 , 所需的动能也就越大 , 这需要提供近乎无限的能量才行 。 但这显然是不可能做大的 , 更不用说超光速了 。
到目前为止 , 人类制造的狙击枪子弹能达到1000米/秒(最多不超过1800米/秒) , 速度最快的航天器是美国“朱诺号” , 速度达到了73600米/秒 。 与光速(299792458米/秒)的差距 , 是四个数量级 , 这让人感到十分的绝望 , 但我们还有机会!
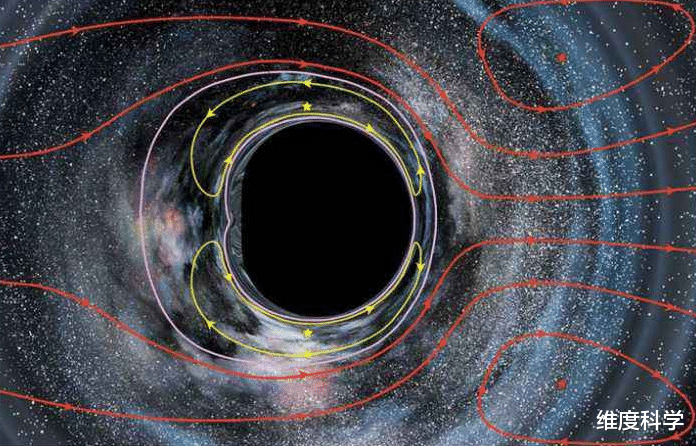
超远距离到达的方法在爱因斯坦的理论没有被推翻之前 , 我们只能在现有的理论框架上 , 找到解决办法 , 所以我们在这里要引进一个新概念——空间扭曲 。 根据爱因斯坦相对论的解释 , 当一个有质量的物体体积无限小的时候 , 所产生的引力就会改变空间 , 造成空间扭曲 。
并且这一现象已经被科学家通过射电望远镜 , 在中子星附近观察到了 。 如果人们能利用空间扭曲 , 或许可以实现超远距离到达 , 从一个地方快速到达另一个地方 。
简单解释起来就是 , 将三维的空间看做一张二维的纸 , 在这张纸的两端画上两个点 , 作为起点和终点 。 在平整的二维纸面上 , 的确是光速物体能最先从起点到达终点 。 但利用空间扭曲 , 也就是把二维纸折起来 , 将起点和终点对齐 , 再钻一个洞(虫洞) 。
物体就算是以正常汽车的速度行驶 , 也能比光速物体通过直线行驶 , 先到达终点 。 这种方法并没有超越光速 , 只是将原本相距甚远的两个时空点 , 用“隧道”连在了一起 , 缩短了距离而已 。
你也可以想象为从起点到终点要翻过一座山 , 在科技落后的情况下 , 只能绕着山走 , 或者爬上去再爬下来 , 翻山走 。 而科技进步后 , 我们学会了挖隧道 , 直接穿山而过 , 速度不改 , 但距离变了 。
总结这种方法在理论上是可行的 , 但又会出现一个新的问题:如何稳定地制造这种空间扭曲(虫洞) 。 我们现在只是能观察到 , 而无法利用 , 想要实现“超远距离航行” , 还需要无数人的努力才行 。
你认为我们能掌握空间扭曲的方法吗?
推荐阅读
- 华夏为何缺失千年文明?中西方神话暗藏玄机,三皇五帝是外星人?
- 龙生活在地球的大气层?它们究竟是真实存在,还是古人的妄想
- SpaceX“货运龙”将为NASA执行第24次空间站货运任务,圣诞节前到
- 北交所开市之后,四大交易所都该怎么玩?
- 高通驶入自动驾驶“深水区”
- 酒后驾车幸存者在同一事件中丧生
- 11月15日北交所就开市了,散户有哪些细节需要注意?
- 湖南:连面都没有见过,男子就给39万彩礼,发现对象就是红娘
- 苍天啊!比威少还铁!75大到底怎么了,不想打就交易吧







