拓扑学 , 英文为 Topology , 最初是几何学的一个分支 。 通常的几何学是研究平面或几何体上点、线、面之间的位置关系以及它们的度量性质;拓扑学对研究对象的长短、大小、面积、体积等度量性质和位置关系都不关心 , 而是研究几何形状在连续形变下的不变性 , 即“拓扑不变性”和“拓扑等价性”等内容 。 在通常的平面几何和立体几何中 , 两个图形等价 , 是要求两个图形通过平移、旋转等操作能够完全重合;在拓扑学里所研究的图形 , 大小、形状都可以改变 , 但是表面的点、线的结合关系、顺序关系应该保持不变 。 如图1 , 粉色的图形通过连续的变形可以从球逐渐变成鸡蛋、表面凹陷的球、类似鸭舌帽的图形等 。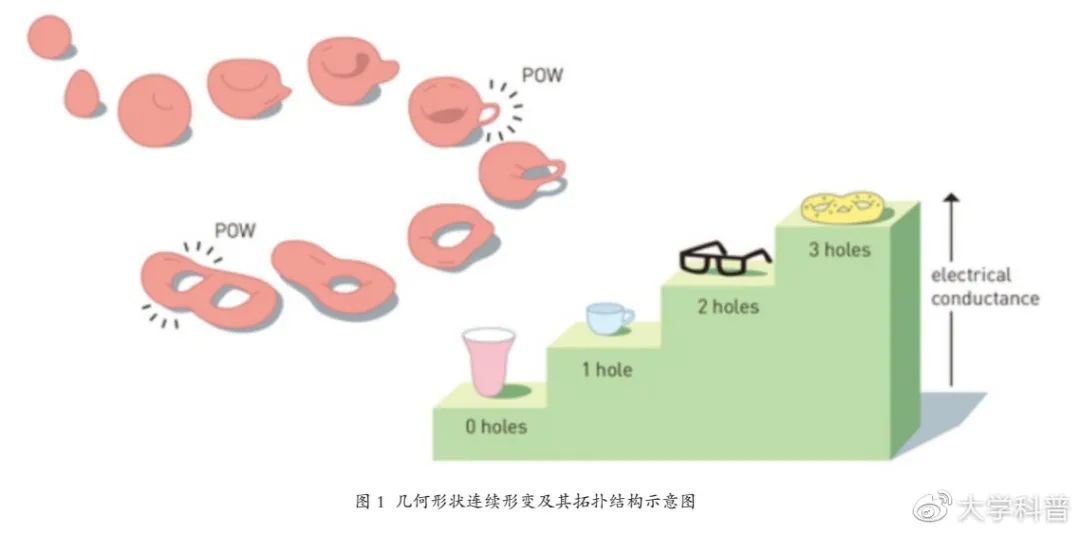
本文图片
在几何拓扑的基础上 , 通过几何的微分形式研究体系的整体性质就是微分拓扑 , 其包含两个核心概念:底流形和纤维丛 。 流形是欧几里德空间的一个子集 , 这个子集不一定是平直的 , 可以是一个平面、一个球面等几何形状 。 底流形 , 顾名思义就相当于我们选取的一个基底空间 。 纤维 , 就是定义在基底空间上的可参数化的空间 。 例如 , 向量空间等 , 而纤维丛就是基底空间与纤维空间的乘积空间 。 例如 , 二维平面可以看成是两个一维平面的乘积 , 圆柱面可以看作是圆圈和一维直线空间的乘积 。 纤维丛的一个形象比喻就是一把卷发梳:底流形是梳柄 , 而纤维则是上面的一根根梳齿 。
微分拓扑已在物理研究中发挥重要的作用 。 例如 , 高能物理中的规范反常和引力反常 , 凝聚态物理中的整数量子霍尔效应 , 分数电荷等 , 都与各种物理空间中的拓扑性质相关 。 拿一个二维体系的电子结构举例:在二维体系中 , 考虑周期性边界条件 , 其动量空间张成了轮胎面状的布里渊区(底流形) , 布里渊区内所有占据态的布洛赫波函数以及布里渊区就构成了纤维丛 , 可以借助微分几何的概念来刻画材料电子结构的拓扑性质 。

本文图片
“拓扑”与磁性的第一次结合是整数量子霍尔效应
1980年 , Von Klitzing等发现二维电子气在极低温条件下 , 随着外加磁场的增强 , 霍尔电导不再随磁场连续变化 , 而是呈现出一个个量子化的平台 , 如图3所示 。 因此项研究 , Von Klitzing获得了1985年的诺贝尔物理学奖 。 在量子霍尔效应体系中 , 材料的边界上会形成一些贯穿能隙的边界态 , 边界态的数目对应于陈数(一种拓扑数) 。 D.Thouless最早利用微分拓扑中的陈数解释了量子霍尔电导平台的稳定性 , 他也因为这一工作获得了2016年的诺贝尔物理学奖 。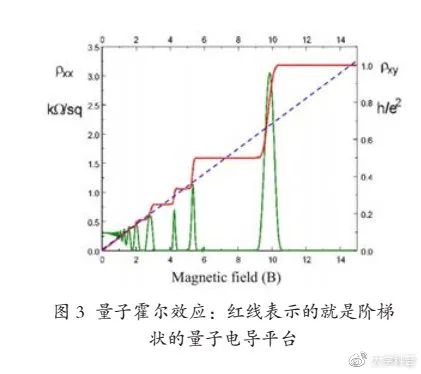
本文图片
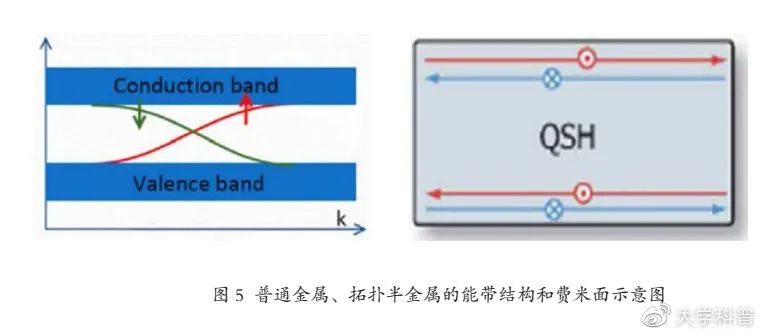
从2005年开始 , 拓扑学的知识在固体物理中得到了广泛的应用 。 Kane和 Mele等在研究二维石墨烯时最早提出了“拓扑绝缘体”的概念 。 二维拓扑绝缘体 , 又称量子自旋霍尔效应绝缘体 , 是一种全新的量子物态 , 它的体态是绝缘的 , 但是在边界上存在拓扑保护的、能够导电的边界态 。 如图4所示 , 量子自旋霍尔边界态具有重要的“自旋过滤”特性:在边界上 , 自旋向上的电子都向右运动 , 而自旋向下的电子向左传播 , 彼此互不干扰 , 可以有效抑制“背散射” 。 因此 , 量子自旋霍尔效应体系在微纳尺度是无电阻的理想导体 。
“拓扑”与磁性的第二次结合是量子反常霍尔效应的实现
量子反常霍尔效应不同于量子霍尔效应 , 它的产生不依赖于外加磁场而由材料本身的磁化产生 。 早在1988年 , Haldane就提出了一种在六角晶格中实现这种无外加磁场的量子霍尔效应的理论模型 , 由此他也分享了2016年的诺贝尔物理学奖 。 2013年 , 薛其坤院士团队在实验上首次观测到了量子反常霍尔效应 , 该工作获得了国家自然科学一等奖 , 其本人也获得了2020年度的菲列兹·伦敦奖 , 成为首个获得这一荣誉的中国科学家 。
本文图片
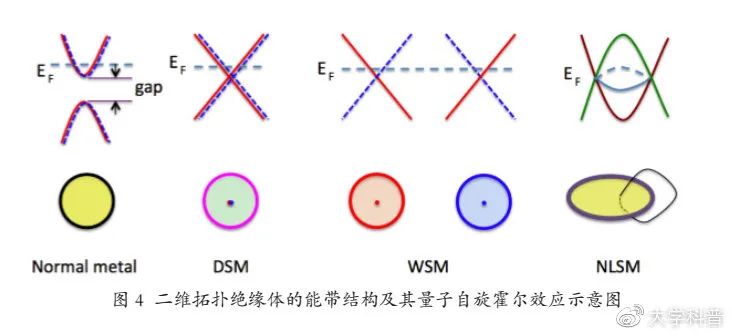
2011年 , 随着对拓扑绝缘体的深入研究 , 人们又发现了拓扑半金属:它的能隙为零 , 费米面是孤立的点或者闭合的线 。 拓扑半金属是不同于拓扑绝缘体的一类新的拓扑量子态 。 根据节点的简并状况及在动量空间中的分布 , 拓扑半金属可以细分为外尔半金属(WSM)、狄拉克半金属(DSM)和节点线半金属(NLSM)等 。 如图5所示 , 前两种半金属的费米面是动量空间中几个孤立的费米点 , 而NLSM中的费米面是一维的闭合环线 。 与拓扑绝缘体一样 , 拓扑半金属也有许多新奇的物性 , 包括动量空间中的磁单极子、费米弧、外尔异常和负磁阻效应等 。
本文图片
“拓扑”与磁性的第三次结合是磁性拓扑半金属
2011年 , 万贤刚等最早预言了烧绿石结构的反铁磁处于一种外尔半金属相 。 随后 , 徐刚等发现了尖晶石结构中铁磁态的三维拓扑半金属 HgCr2Se4 。 自此 , 越来越多的磁性Weyl半金属材料相继提出 , 包括Heusler化合物、Kagome层状材料和蜂窝状晶格材料等 。 与此同时 , 对于磁性Dirac半金属材料的研究也获得广泛关注 , 包括CuMnAs、EuCd2As2等材料体系被相继提出 。 磁性NLSM体系包括层状的Fe3GeTe2和LaCl等 。 这里我们选取EuCd2As2体系作为磁性拓扑半金属的例子 , 简单介绍其新颖的拓扑物性 。 EuCd2As2是一种具有层间反铁磁结构的狄拉克半金属 , 在费米能级上只存在一对狄拉克点 , 如图6所示 。 通过调整磁矩方向 , 在EuCd2As2中还可以实现轴子绝缘体等新奇拓扑物态——在其某些表面上可以打开表面态的能隙 , 实现半整数量子霍尔效应、拓扑磁电效应、轴子极化激元等物理现象 。 EuCd2As2的发现为研究拓扑相变和新型反铁磁拓扑物态提供了一个理想平台 。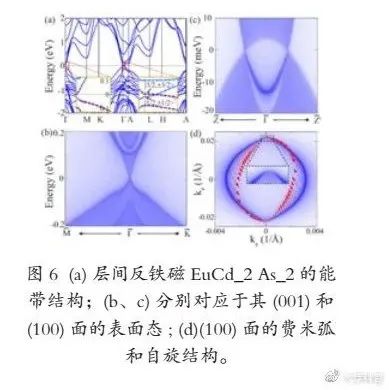
本文图片
相比于非磁拓扑材料 , 磁性拓扑材料最大的优势就是通过外加磁场可以有效调控磁性拓扑材料的磁化方向 , 从而实现不同拓扑态之间的拓扑相变 。 例如 , 外加磁场可以实现磁性拓扑半金属到“量子反常霍尔态”、轴子绝缘体的转变 。 这些拓扑转变可以巨大地改变材料的物理性质 , 可以用来设计拓扑电子学器件 。 除了电学、磁学方面的新奇物性 , 磁性拓扑材料在光学等其他领域也有应用 , 包括实现拓扑磁光效应、用于宇宙暗物质探测等 。
与拓扑相关的研究还包括高阶拓扑绝缘体、非厄米系统中的拓扑态、磁性-超导材料异质结中的拓扑超导态等 。 这些前沿研究具有广泛而深远的战略意义 。 其中 , 拓扑与磁性的结合尤为重要 。 一方面它可以提升我国的科研创新能力 , 另一方面相关量子现象的探测和调控研究将为新一代自旋电子器件、量子通信、拓扑量子计算机等领域打下坚实的理论基础和材料基础 。
作者简介:徐刚 , 教授、博士生导师 。 2010年获中国科学院物理研究所博士学位 , 2010-2012年任中科院物理所助理研究员 , 2012-2016在美国斯坦福大学做访问研究 , 2016年至今在华中科技大学国家脉冲强磁场中心工作 。 2017年入选国家人才计划青年项目;2018年获科技部重点研发计划青年项目(项目负责人);获“2018年度中国科学院杰出科技成就奖(集体)” 。 主要从事新奇物性和材料的第一性原理计算和理论研究 。 研究兴趣包括:强关联与非常规超导、拓扑物质态 , 新型二维功能材料等 , 已发表学术论文50余篇 , 其中Nature子刊 , PRL等国际顶级期刊20篇 , 总引用7500多次 ,H因子29 。
来源:《大学科普》“理论物理”科普专题
【科学|“拓扑”与磁性的结合】编辑:荔枝
推荐阅读
- 快报|“他,是能成就导师的学生”
- 技术|“2”类医械有重大进展:神经介入产品井喷、基因测序弯道超车
- bug|这款小工具让你的Win10用上“Win11亚克力半透明菜单”
- 重大进展|“2”类医械有重大进展:神经介入产品井喷、基因测序弯道超车
- 历史|科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 空间|(科技)科普:詹姆斯·韦布空间望远镜——探索宇宙历史的“深空巨镜”
- 精度|将建模速率提升10倍,消费级3D扫描仪Magic Swift在2021高交会大显“身手”
- 四平|智慧城市“奥斯卡”揭晓!祝贺柯桥客户荣获2021世界智慧城市治理大奖
- |南安市司法局“加减乘除” 打造最优法治营商环境
- ASUS|华硕预热ROG Flow Z13:称其是“全球最强悍的游戏平板”







