定理|初二数学下册：三角几何解题4步走综合题|性质|图形|概念|几何

什么是三角形
不在同一直线上的三个顶点、两两用线段联结起来的图形叫三角形。它有三个内角、三个外角、三条边，还有三类特殊的线：角平分线、中线和高。
三角形是最简单的多边形，它正如“家庭是社会基本的细胞”这句话一样，在几何学中寓意深刻。
三角形知识只有八年级用得到吗
No ，它几乎贯穿整个初中、乃至高中阶段的几何学习，并且在以后的几何学习中会频繁出现，可谓“魅影重重” ，能熟练掌握并灵活应用三角形性质、定理来破解几何难题，是每个初中、乃至高中生必须修炼的武林绝技。如果说“得梅长苏者得天下” ，那么“得铁三角者得几何”应不是妄言。
八年级三角形相关知识点有哪些？

1、三角形的概念与性质；
2、全等三角形的性质与判定；
3、等腰三角形的性质与判定 .

然而在所有上述知识点的学习和解题的过程中，同学们通常会出现这样一种感觉：一听就懂，直观而简单的习题一上手就OK 。但是一碰到复杂的综合题，顿时“拔剑四顾心茫然”——宝刀我有，然鹅何处入手？
几何综合题型一般有这样的特点：图形复杂，线条多、角度多，且貌似与求证结果完全风马牛不相及也。而这类题在期末考中必有，甚至在至关重要的中考中也必有，同学你若只管用无神的双眼漠视它，不调动你最强大脑中的风暴横扫它，结果就只能在考试中弃题、丢分，并因此与高分和满分失之交臂。
“王者农药”尚需苦练绝招，学海争霸岂可只凭撞运侥幸！
今天，我们就针对综合性三角形几何求证题，给大家来讲解一下遇到这类题型，应该遵循什么样的解题思路、逻辑方法以及基本攻略。
首先，解综合类三角形几何题，有哪些注意事项呢？
第一、熟记并理解三角形的概念、分类、性质以及三角形全等的判定（这是必须的——必正背、必倒背）。
第二、学会在复杂的图形中分离出表示某个几何概念的那部分图形（这是要训练的——必各种看、必各种画）。
第三、熟练并灵活地运用上述知识进行计算、说理以及解决问题（这是需要攻略和实训的——必潜心琢磨、必有效刷题）。
我们来看一道综合类的三角形几何题，感受一下如何灵活应用相关的知识点，逻辑清晰、条理分明地解题。
如图1所示，已知：∠1=20° ， ∠2=60° ， ∠3=10° ， ∠EBC=70° ，求∠DEB .

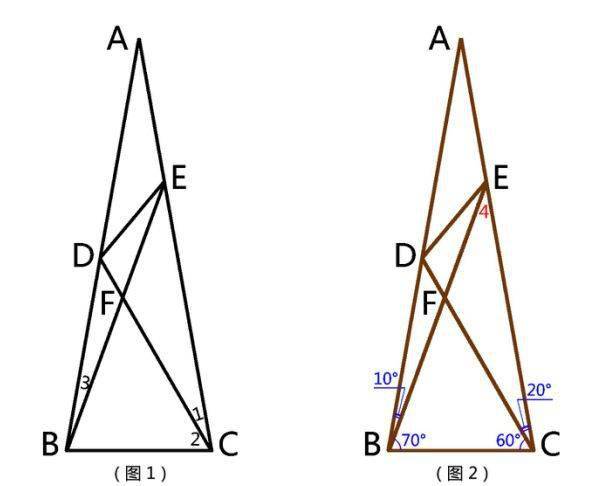
文章图片

解题基本攻略如下：
第一步：草稿标图（以重要性而言， “解几何前的标图”绝不亚于“发自拍前的P图”）。
养成标图的好习惯，是几何高效解题的第一步；学会标好图（读题、审题、整理思路全在里面了），你的破解将事半功倍。
好，现在我们先尽可能将已知条件标注在图上（如图2），这一来，立马就直观地看出图形的以下特点：
【定理|初二数学下册：三角几何解题4步走】1、∵∠ABC=10°+70°=80° ， ∠ACB=20°+60°=80°
∴∠ABC=∠ACB ， △ABC是等腰三角形
2、∵∠A=180°-∠ABC-∠ACB=20°
∴∠BEC=∠A+∠3=30°（即∠4=30° 。该角与所求角度相邻，值得关注）

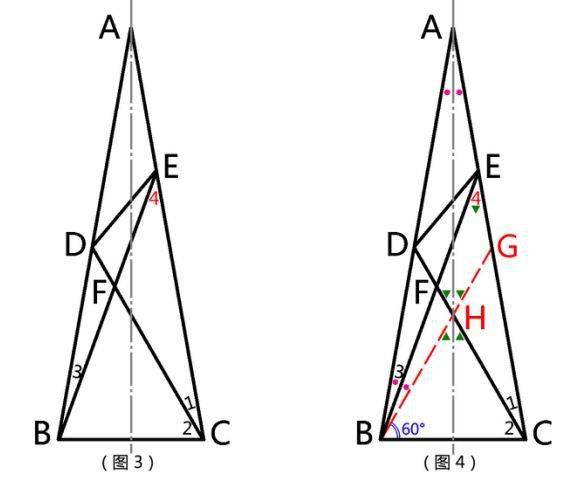
文章图片

第二步：快速默念所有相关概念、定理——尤其是重要性质或定理（迅速锁定有用的定理，正如比武在即，务必精选一件趁手的大杀器）。
这也充分说明：如果概念模糊、知识点缺失，要破解综合性压轴难题的概率——那是飞流直下三千尺——直接到零了。
即如此题，它有什么重点性质呢？便是那个在等腰三角形对称轴上的“三线合一” 。所以速度在草图上继续标出△ABC的对称轴（图3），看看会有那些玄机？
玄机1：发现四个与∠4相等的角（图4中绿色三角标记处）。
在贯穿初高中几何的所有知识点中， 30°、45°、60°……这些特殊角永远是解题过程中值得我们特别关注的。所以，当对称轴出现后，我们一眼可以看到它与∠2这个60°角的一条边相交于一点（我们设它为H），由该三角形的对称性可知：连接B、H并延长BH交AC于G ，那么△HBC不仅等了腰，而且等了边。 So ，该四角均为30° 。
玄机2：发现三个与∠3相等的角（图4红色圆点标记处）。
因为轴对称，所以20°的顶角∠BAC被均分为两个10°的角。又因为原为70°的∠EBC被刨去一个60°角后，剩下的领地∠EBG也只有10°的狭窄空间了。
玄机3：两两相邻的10°角组成了某三角形相等的底角。
∠BAC忽然与∠ABG成了绝配，并稳稳地指向了他们各自对应的、同样般配的腰：AG=BG
上述三大玄机的出现，还不足以让你思潮起伏、浮想联翩吗？须知刚学过本学期几何的重头戏“三角形全等”哦，有相等的角，还有相等的边，全等三角形已然呼之欲出了。
缓一缓，让我们整理一下思路，在草图上继续划划看——果然，终于等到你、全等三角形！

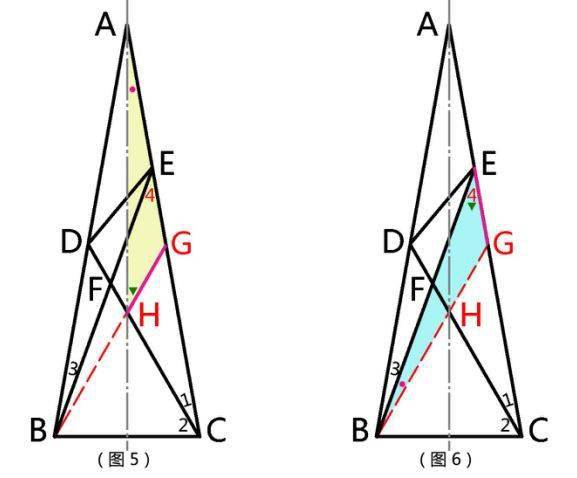
文章图片

第三步：找出全等三角形中那组有用的对应元素（春风十里，不如遇到那个善解人意的你）。
见图5与图6 ，一番甄别，毫无疑义，这里最具含金量的全等三角形对应元素是：GH=GE ，因为我们终于将所求的角∠DEB缩小到小范围四边形DHGE的可控包围圈中了。
第四步：直击终极目标（是时候关门、亮灯，让目标宠物汪暴露在低碳、节能、环保的LED灯下了）。

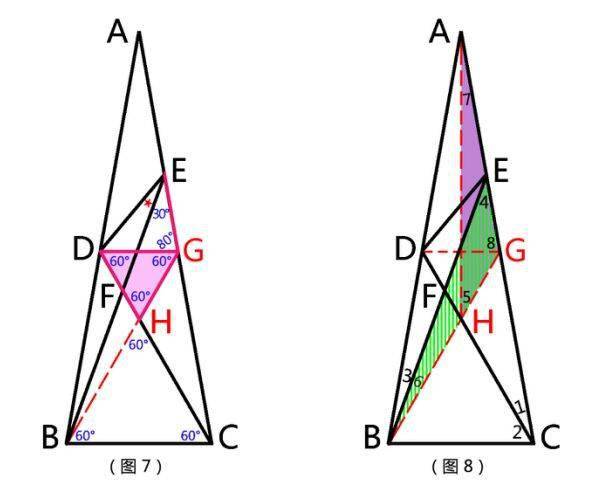
文章图片

该关的门窗一个都不能少，包围圈就要越小越好。我们很容易发现：在四边形DHGE这个两房两厅平面图中， △DHG不仅等着腰，而且等着边，那就意味着GH=HD=DG ，而刚才我们发现GH=GE 。
Now ，关闭客厅通道，继续缩小范围，就只剩下△DGE了，且DG=GE ，易证∠8=80° ， ∴∠DEG=50°→∠DEB=20° 。
Game 就这样over 了。
纵观整个解题过程，你有木有发现：夺高分、争学霸、解几何——学会标图绝对比学会P图重要的多得多得多？
几何综合性解答题的求解方略，总结一下：
1、习惯标图，学会标图！学会标好图！！学会有效标好图！！！
2、像背乘法口诀一样背出几何性质，像卖油翁随手灌油那样信手拈来有用的几何定理——确保精准无误！
3、缩小包围圈，逐步向目标靠拢，而后一击而中。
这道题的考点涵盖了：
<1>等腰三角形的性质：等角对等边，三线合一.
<2>等腰三角形的轴对称性质。
<3>全等三角形的判定：A.A.S.
<4>等边三角形的判定：有一角为60°的等腰三角形是等边三角形.
<5>三角形内角和定理：三角形内角和为180°.
end
声明：本文内容来源于网络，转载请联系原出处。初三研究中心尊重版权，如有侵权问题，请及时与管理员联系处理。
点击 "阅读原文" 加中考君微信好友哦