宇宙的基础是对称吗？群论给了我们答案

文章图片

物理学家从最基本的层面研究宇宙是如何运作的。如果你问物理学家：是什么让宇宙运转起来？物理理论的核心是什么？常见的答案之一是对称性。
对称性是物理学的核心，它似乎是宇宙的基本属性，并导致了一些深刻的定律。每个对称都会导致一个守恒量，例如导致能量守恒、动量守恒和电荷守恒。它甚至会导致基本力的产生，如电磁力、弱力和强力。那么，什么是对称？它在物理学中如何发挥作用？
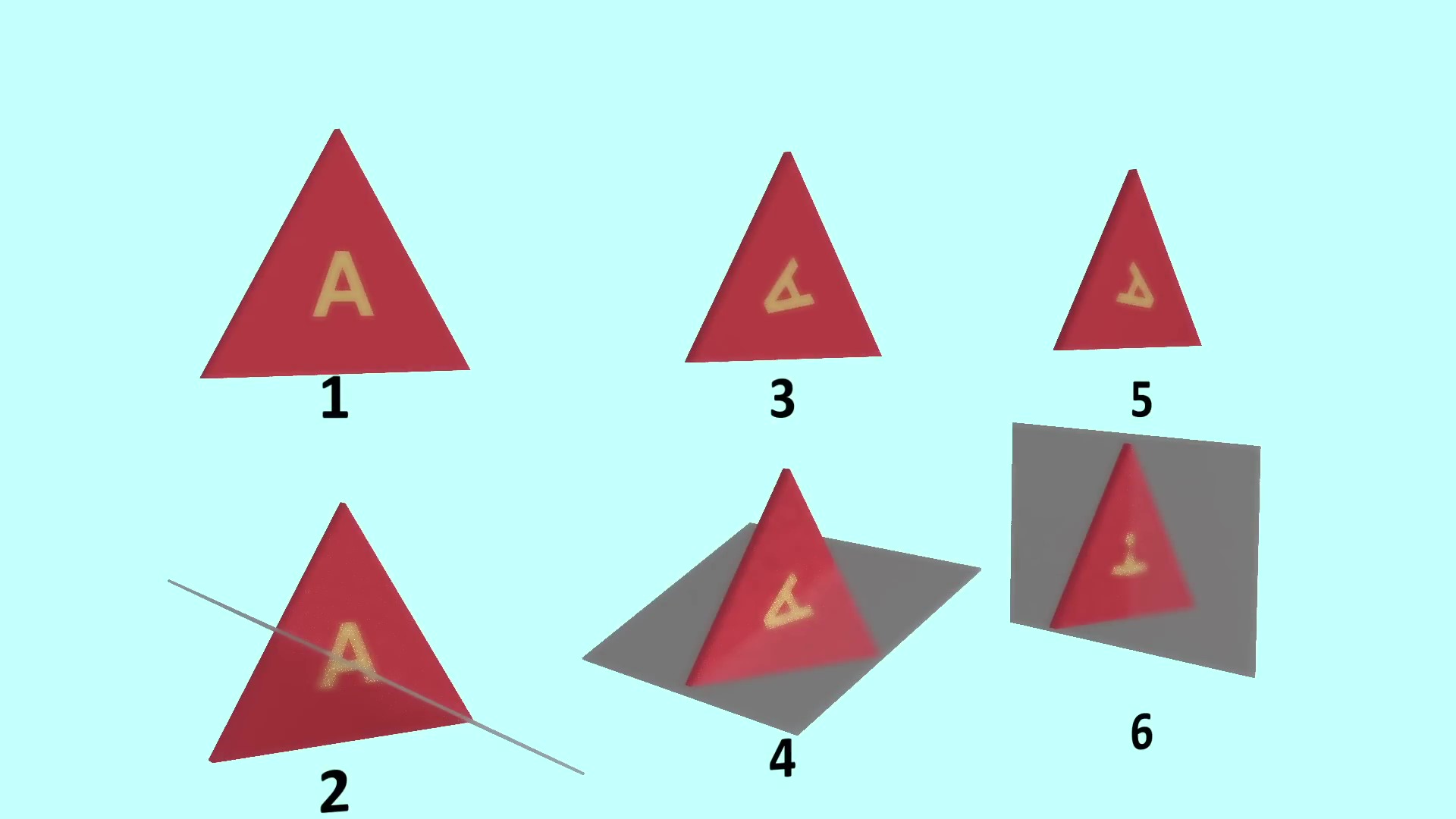
什么是对称我们已经在小学的一堂课上学习过对称性。考虑一个等边三角形，如果我们在其任意一条中线处放置一个镜子，那么另一半和镜子中的像连起来也会是一个相同的等边三角形，这就是等边三角形的一种对称。此外，我们还可以执行另外一种操作，将它绕着形心旋转120度，会得到原始的等边三角形，这是等边三角形的另一种对称。我们如果把这些对称都列出来，那么我们可以得到六种排列方式。

事实上，我们刚才谈到的是一个复杂东西的简单例子，即群论。群论是对称背后的数学。等边三角形的对称性背后的数学称为3次二面体群，其中3是指具有三个角的三角形。我们也可以说它是6阶的，因为有6个排列，也称为群元素。再举一个例子，如果我们考虑正方形的对称性，其背后的群论将是4次二面体群。
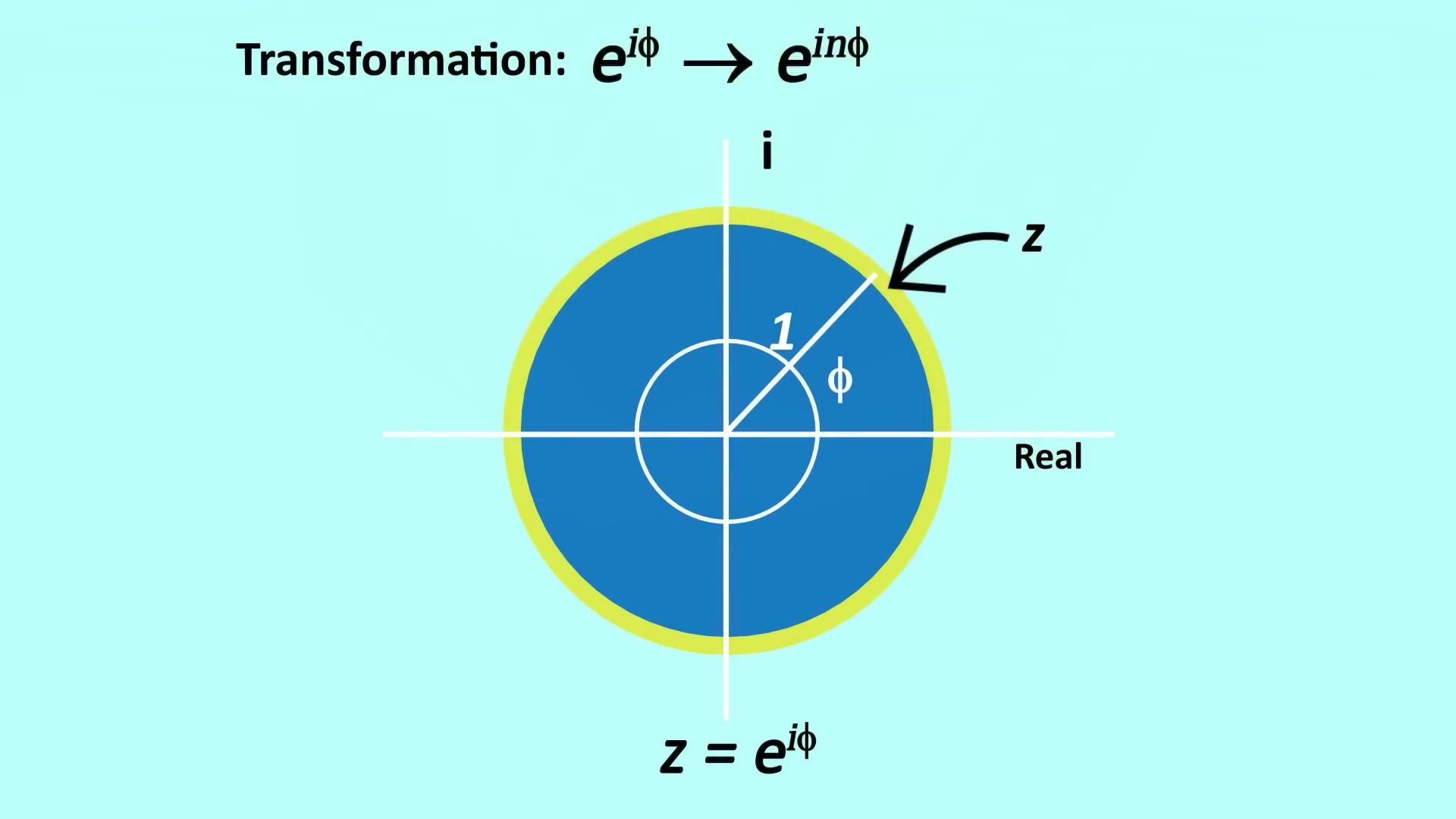
U(1)如果多边形的边数是无限的呢？我们得到一个圆。一个半径为r的圆在笛卡尔坐标下可以这样表示：x=rcosΦ ， y=rsinΦ 。如果使用极坐标来描述，我们就可以使用复数来表示圆，可以只用一个方程来表达：z=re^iΦ 。如果我们选择半径为1 ，那么事情会变得更加简单，如下图。

这个单一的复数z可以描述半径为1的圆上的任何点，我们要做的就是将其中一个轴更改为虚数轴，所以圆在复平面上。请注意，圆上的点由完全由角度 Φ决定。事实证明，有一个对称群与这个半径为1的复数圆相关联，它被称为U(1)群。该群的元素是围绕圆的所有无限可能的角度Φ 。所以我们可以将U(1) 群的变换形式写成如下图所示，其中n是生成器， n代表我们围绕圆旋转了多少。

我们在哪里见过物理学中的复数？在量子力学中，它建立在复数之上。让我们尝试通过这个简单的变换来应用绕圆移动的对称性。为了描述作为物质粒子的费米子，我们需要一些运动方程来描述它的行为。为此，我们可以使用狄拉克方程。
U(1)在物理的应用在狄拉克方程中， L是拉格朗日量，它只是粒子动能和势能之间的差。 ψ是物质粒子的波函数， ψ上面一杠是等效反物质粒子的波函数。括号的第一部分描述了粒子在时空中的运动，第二部分m是质量。所以，这个方程描述了一些质量为m的物质粒子在空间中的移动。

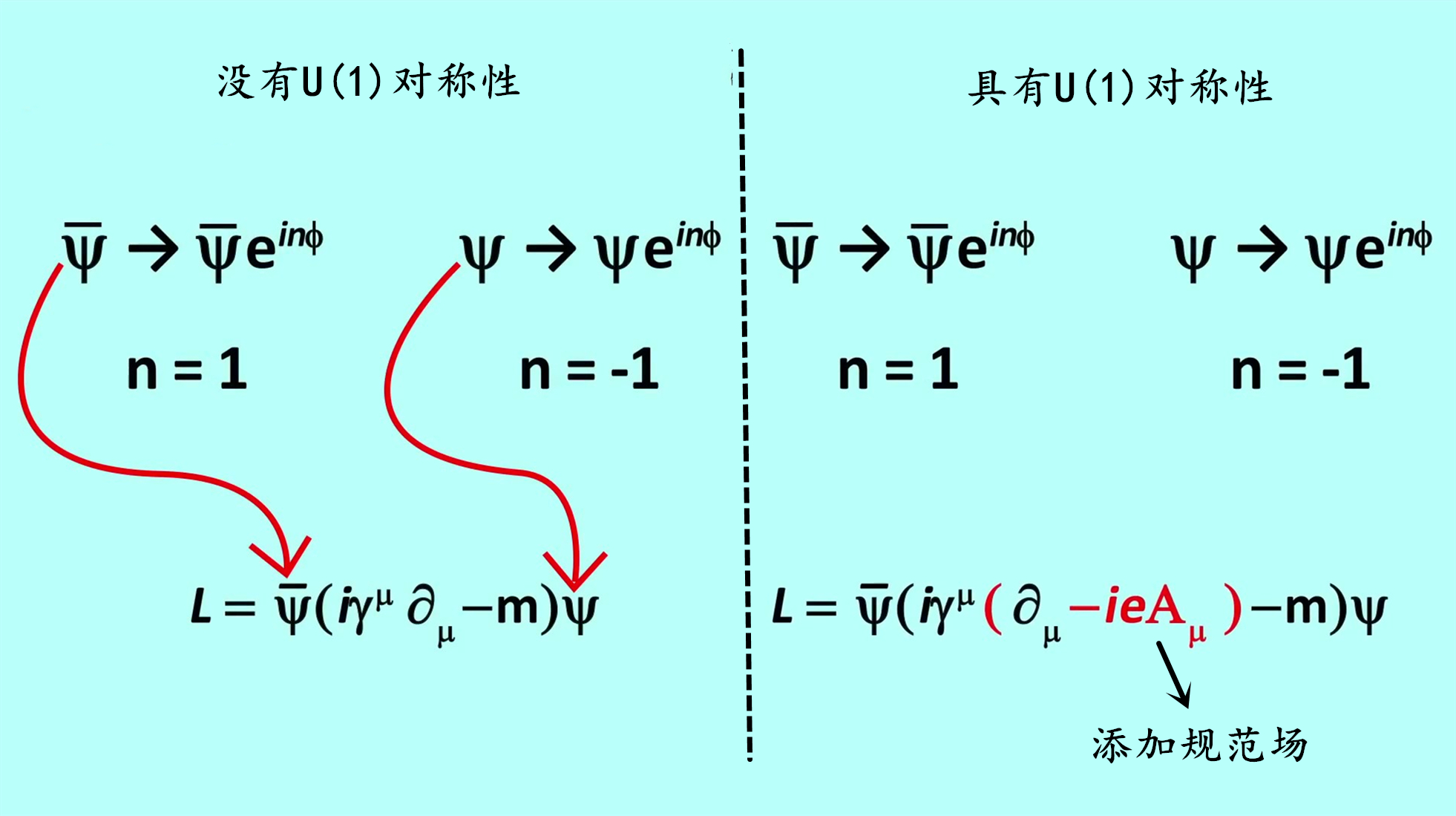
接下来就是群论的用武之地，如下图所示。如果存在U(1)对称性，这意味着如果我们将变换应用于方程，那么拉格朗日量不会改变。问题是，当我们这样做时，拉格朗日量确实发生了变化，所以这告诉我们它没有U(1)对称性。然而，如果我们修改方程，在理论中增加一个新的量子场，即所谓的规范场，那么我们就可以有一个对称性。规范场的另一个名称是力，因此当我们向方程中添加力时，我们会发现存在对称性。然后我们的理论就起作用了，并且具有U(1)对称变换。

那么我们刚刚添加的这个力是什么？事实证明，添加到方程中的这个新术语描述了电磁力。这里的字母“e”是电荷， A_μ代表光子场。这告诉我们，光子是介导电磁力的粒子。因此，虽然我们在狄拉克的初始方程中有电子，但没有相互作用。而修改后的方程里有一个电子和电子相互作用的方程，它是由光子场介导。完整的方程如下所示，其中前面这一项已经在前面文章中介绍过。

我们采用了费米子理论并要求对 U(1) 进行变换，添加额外的数学术语以使对称起作用，为我们提供了由光子在费米子之间介导的电磁力，这就是电磁力理论，也称为量子电动力学或 QED 。

宇宙的基础是对称吗？群论给了我们答案

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)