文章图片

文章图片

文章图片

进入黑洞的东西都去了哪?
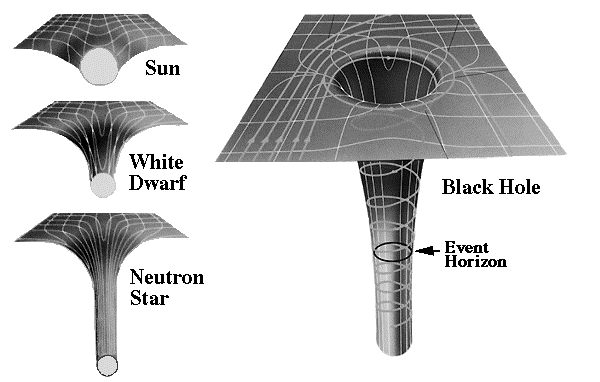
图源网络 翻译左图自上而下:太阳 白矮星 中子星 右图:黑洞 事件视界
拿常见的“橡胶板”类比 , 一个巨大的引力物体扭曲了时空“织物”的恒定时空“切片” , 就像蹦床上的重物把它压低一样 。
一个黑洞的“洞”的集中质量很大 , 以至于它把“蹦床”无限拉伸 , 在“织物”上“撕开一个洞” 。 拉伸在事件视界上变得无限 , 质量不知何故驻留在视界内 , 从外部观察就“超过”该点 。
(有次我的物理老师告诉我:“自然界中没有无限的东西” 。 如果真的是这样 , 那么计算机上的“ERR”就不是实际存在的 。 但这是迄今为止最好的解释 。 )
接近黑洞的粒子永远不会到达事件视界 , 因为它们距离无限远 。 而实际的度量 , 可测量的粒子向内到达视界的距离在理论上是无限的 , 时空的结构是无限的扭曲 。 即使粒子以光速向内坠落 , 时空的结构也是无限地被拉长了 。 仅仅为了到达事件视界的航行就已经如此艰难 , 更不用说在黑洞里面的事情了 。 即使假设你以超光速的速度航行 , 你甚至永远无法到达事件视界 , 更别提通过它 。
所以要是回答这个问题 , 任何掉向黑洞的东西 , 就只是保持坠落落落落落......空间无限地延伸(“向下”或“向外”通过我们熟悉的3D之外的一些更高的超维) , 无限地接近事件视界 , 但永远距离事件视界无限远 。
(从理论上讲 , 质量本身已经“延伸得更远” , 并驻留在“时空结构之外” 。 )
这是一个非常重要的问题 , 大多数物理学家都没有尝试回答 。 但是深入对黑洞结构的理解有助于思考这个问题 。
引力伴随着时间延缓 , 这意味着引力会影响大质量物体附近的时间流动 。 这个现象甚至在地球上也存在——由于在地球表面附近的时间流动比在太空中的时间流动要慢 , 因此 , 将卫星的时钟与地面时钟同步存在很多问题 。 这也是所有最初的通信卫星都失败了的原因 。 后来 , 专家们在卫星的时钟上编入一个补偿器 , 以便它们能够与地面通信一起工作 。
由于黑洞巨大的引力 , 黑洞呈现出时间延缓的极端情况 。 (你需要把多个概念在脑海中理清才能理解) 。
光速是宇宙的最大速度限制 。 由于光速是有限的 , 实际上我们生存的是一个更古老的宇宙 。 例如:来自太阳的光需要8分钟才能到达地球 , 所以我们现在看到的太阳不是太阳 , 而是8分钟前的太阳但是如果太阳突然消失了 , 我们需要8分钟才能意识到太阳已经消失了 。 同样地 , 距离我们最近的恒星的光需要四年才能到达地球 。 所以我们看到的恒星不是真正的恒星而是四年前的 。 仔细想想 , 我们其实实际上是在回顾过去 。
现在尝试理解这个说法 。
引力影响空间——它可以弯曲、拉伸和压缩空间 。 黑洞的巨大引力能把空间极端弯曲 。 当我们根据科学家的说法观察黑洞的性质时 , 他们清楚地指出 , 随着已知的物理定律的崩塌 , 黑洞的内部条件是不可知的 。 这个情况是不是似曾相识?大爆炸前也是这样 。
我们还需要看看关于黑洞的科学研究 。 其中最著名的是爱因斯坦场方程 。 但也有特殊情况 。 当求解爱因斯坦场方程时 , 我们得到施瓦茨柴尔德度量 。 施瓦茨柴尔德度量的完整几何由一个黑洞、一个白洞和两个在它们的事件视界上通过虫洞连接的宇宙组成 。 施瓦茨柴尔德虫洞就是爱因斯坦方程的精确解 。 白洞是黑洞的对立面 , 白洞并不会像黑洞那样用引力拉入物质 , 而是抛出物质 。 根据施瓦茨柴尔德度量 , 所有落入黑洞的物质都会通过虫洞 , 然后被抛出白洞 。
或许这就是你的答案:“被吸进黑洞的物质穿过虫洞 , 到达白洞 , 然后被抛出” 。
但不要仅止于此 , 我们要验证一下自己的答案 , 并且证明是否真的有这样的白洞 。
现在 , 总结一下上面的要点:
推荐阅读
- 疑似曾被UFO击碎的“车里雅宾斯克陨石”微粒中,发现奇特的晶体!
- 如果恐龙没有灭绝,世界会变成什么样子?能与人类和谐共处吗?
- ?2.7亿光年外,哈勃发现星系大碰撞,这是45亿年后银河系的结局
- 24亿年前的地球是什么样子?如今什么原因导致地球氧气浓度的降低
- 吞噬星空:“洪”一生不愿提及的糗事,面对罗峰的时内心太过尴尬
- 地球大气中的氧将于10亿年后耗尽
- ?北极圈“发高烧”!温度飙升至48℃,地球正疯狂吸热
- 疑似曾被UFO击碎的“车里雅宾斯克陨石”微粒中,发现奇特的晶体







