单射满射双射的区别是什么？

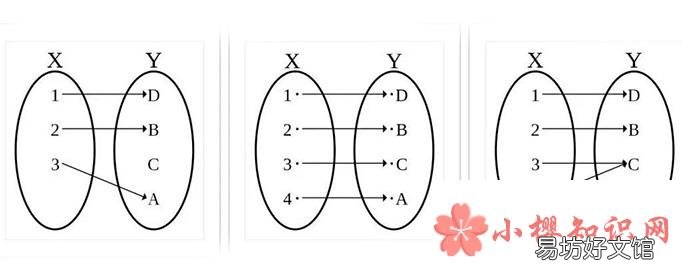
单射只能一对一，不能多对一，满射就是不论一对一，还是多对一，在映射f:X→Y中， Y中任一元素y都是X中某元素的像，也就是Y中所有元素在X中都能找到原像，至于找到的只有一个原像,那就是双射，但有的可以找到一个以上的那就不是双射，即双射就是既是单射又是满射。

文章插图
设f是由集合A到集合B的映射，如果所有x,y∈A,且x≠y ，都有f(x)≠f(y),则称f为由A到B的单射。在数学里，单射函数为一函数，其将不同的引数连接至不同的值上。更精确地说，函数f被称为是单射时，对每一值域内的y ，存在至多一个定义域内的x使得f(x) = y 。另一种说法为， f为单射，当f(a) = f(b) ，则a = b(若a≠b ，则f(a)≠f(b)) ，其中a、b属于定义域。单射在某些书中也叫入射，可理解成“原不同则像不同” 。
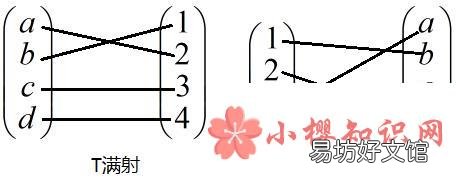
【单射满射双射的区别是什么？】如果每个可能的像至少有一个变量映射其上(即像集合B中的每个元素在A中都有一个或一个以上的原像) ，或者说值域任何元素都有至少有一个变量与之对应，那这个映射就叫做满射。

文章插图
既是单射又是满射的映射称为双射，亦称“一一映射” 。双射(Bijection)的原理是一组关系，在判别某一种想法在应用能否双向的找到某一唯一对应的事物，理论上通常要判断这种想法是否满足双射的关系。因为具体的实施这一想法的途径我们是并不知道的，所以需要抽象出他们的关系，找到这个双射，如果找不到，并且验证这个双射不存在，那么想法是不可能实现的。

文章插图
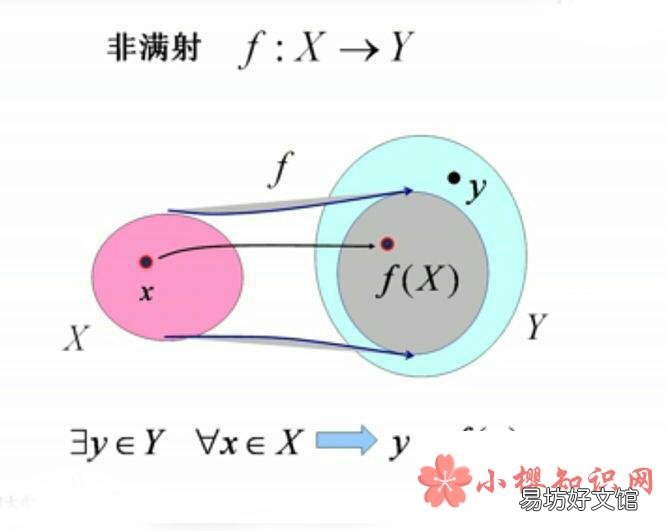
单射(injection):每一个x都有唯一的y与之对应，满射(surjection):每一个y都必有至少一个x与之对应，双射(又叫一一对应,bijection): 同时满足单射与满射，也就是常见的函数映射。那么通俗的说，单射就是只能一对一，不能多对一，满射就是不论一对一，还是多对一，在映射f:X→Y中， Y中任一元素y都是X中某元素的像，也就是Y中所有元素在X中都能找到原像，至于找到的只有一个原像,那就是双射，但有的可以找到一个以上的那就不是双射，即双射就是既是单射又是满射。总之只能一对一或多对一，但不能一对多，并且在映射f:X→Y中X的每个元素都参与， Y中可能都参与，那就满了，就是满射，反之就不是满射。