
文章图片

文章图片
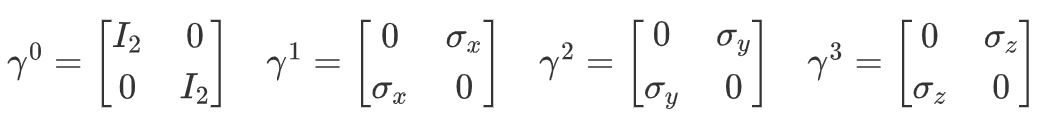
文章图片
狄拉克方程由英国物理学家保罗·狄拉克于1928年推导出来 , 仅在薛定谔提出他著名的薛定谔方程两年后 , 该方程如今已成为量子力学的核心方程之一 。
为了了解狄拉克方程 , 我们首先要了解他试图解决什么问题 。 要做到这一点 , 我们必须回到1905年 , 爱因斯坦用他的狭义相对论改变了世界 。 他提出了光速不变原理 , 光速是我们无法跨越的速度极限 。 此外 , 他将空间和时间统一起来引入了时空 。 他意识到 , 要描述接近光速运动的物体 , 我们必须将时空视为一个统一的实体 。 因此 , 我们必须平等对待空间和时间 。
这是薛定谔方程问题的症结所在 。 如果我们看一下没有任何势的薛定谔方程 , 也就是自由粒子的方程:
我们会看到在方程左边有一个关于空间的二阶导 , 由拉普拉斯算子表示 。 而在方程右边 , 我们有一个关于时间的一阶导数 , 因此薛定谔方程没有平等地对待空间和时间 。 这就是薛定谔方程不适用于描述时空的原因 , 因此也不适用于描述快速运动的物体 。 这意味着薛定谔方程无法与相对论方程兼容 , 不能正确描述接近光速运动的物体 。
与薛定谔方程大约在同一时间 , 有一个量子方程可以兼容相对论 , 它就是克莱因-戈登方程 。 最初在1926年提出它可以描述电子 , 然而事实并非如此 , 我们发现的唯一遵从克莱因-戈登方程的粒子是希格斯玻色子 。 这个方程可以写成如下形式:
关于这个方程的重要一点是 , 现在时间是二阶导 , 空间也是二阶导 。 因此 , 该方程将空间和时间平等对待 , 所以它可以作为考虑时空的相对论方程 。
然而 , 克莱因-戈登方程的问题在于它不能描述电子 , 它描述了自旋为0的粒子 , 如希格斯玻色子 。 克莱因-戈登方程的问题之一是它是二阶的 。 我们都知道 , 如果取一个实数并平方它 , 那么会得到一个正数 。 例如2的平方和-2的平方都等于4 , 但我们不知道最初哪个符号是正确的 , 因此我们会丢失信息 。
事实证明 , 描述半整数自旋的粒子的方程是一阶的 , 因此关于时空只有一阶导数 , 而不是二阶导 。 然而这个二阶结果是相当自然的 , 因为在狭义相对论中能量本身的定义是二阶的 。 解决方案似乎很简单 , 我们只需对克莱因-戈登方程取平方根 。 然而事实证明 , 我们正在寻找的一阶方程实际上是一个具有虚数的复方程 , 而克莱因-戈登方程只有实数分量 。
这就是狄拉克方程的背景故事 , 让我们看看狄拉克是如何解决它的 。 正如我们已经意识到的那样 , 解决方案是以某种方式取克莱因-戈登方程的平方根 。 最初狄拉克提出了以下解决方案:
首先 , 这个方程有点像薛定谔方程 , 也有点像克莱因-戈登方程 。 因为在这种形式下 , 它基本上就是薛定谔方程和克莱因-戈登方程的平方根的杂交 。 在方程等号的左边 , P表示的是动量算子 , 动量的定义是空间分量的一阶导数 。 在方程等式的右边 , 它看起来就像薛定谔方程 , 有时间分量的一阶导数 。 因此 , 在这个方程中 , 空间和时间都是一阶的 , 这正是我们需要的 。 这是狄拉克最初的提议 , 也是最初的狄拉克方程 。
但是我们仍然没有真正解决这个问题 , 因为我们没有弄清楚β和α1、α2、α3的值应该是多少才能让方程起作用 。 事实证明 , 这两个参数是费米子方程的魔力 。 他们最终代表一个自旋向上和自旋向下的粒子 , 以及一个自旋向上和自旋向下的反粒子 。 因此 , 狄拉克用他的方程预测了反粒子 。
最初没有人相信这样的反粒子 , 因此一致认为狄拉克方程是错误的 。 但是 , 仅仅几年后的1932年 , 正电子或反电子就被发现 , 完全符合狄拉克方程的预测 。 在现代 , 我们用所谓的伽马矩阵来编写狄拉克方程 , 可以通过求解β和α参数获得这些矩阵 。
在这些伽马矩阵的帮助下 , 我们可以用更熟悉和紧凑的形式编写狄拉克方程 , 而无需这些神秘的β和α参数:
此外 , 这种写法没有Σ符号 , 利用爱因斯坦的规则“重复指标表示求和” , 其中重复的是上指标和下指标μ 。 μ代表的是时空的每个分量:t和x、y、z分量 。
推荐阅读
- 管道中塞满钢珠,推动其中一端,另一端瞬间掉落,超光速了吗?
- 反方向飞行的两束光,相对速度是两倍光速吗?
- 世界上最好看的十部科普书,有小孩子的一定要看呀!
- 用通俗易懂的方式,解释狭义相对论,爱因斯坦真是太伟大了
- 相对论:卫星上的时间变快了,为什么会变快,时间的本质是什么?
- 光飞行一年的距离是一光年,但光飞行一光年真的不需要一年!
- 爱因斯坦获诺贝尔奖为什么不是相对论,而是光量子假说,他太强大
- 日就月将-科普-天文篇-宇宙
- 盘点宇宙中十大“奇怪”的理论!







