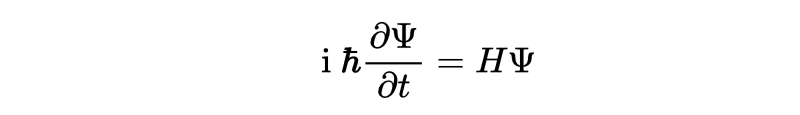
你是如何理解“质量缺口假设”的？还有比这更难的问题吗？ _物理学家

文章图片

文章图片

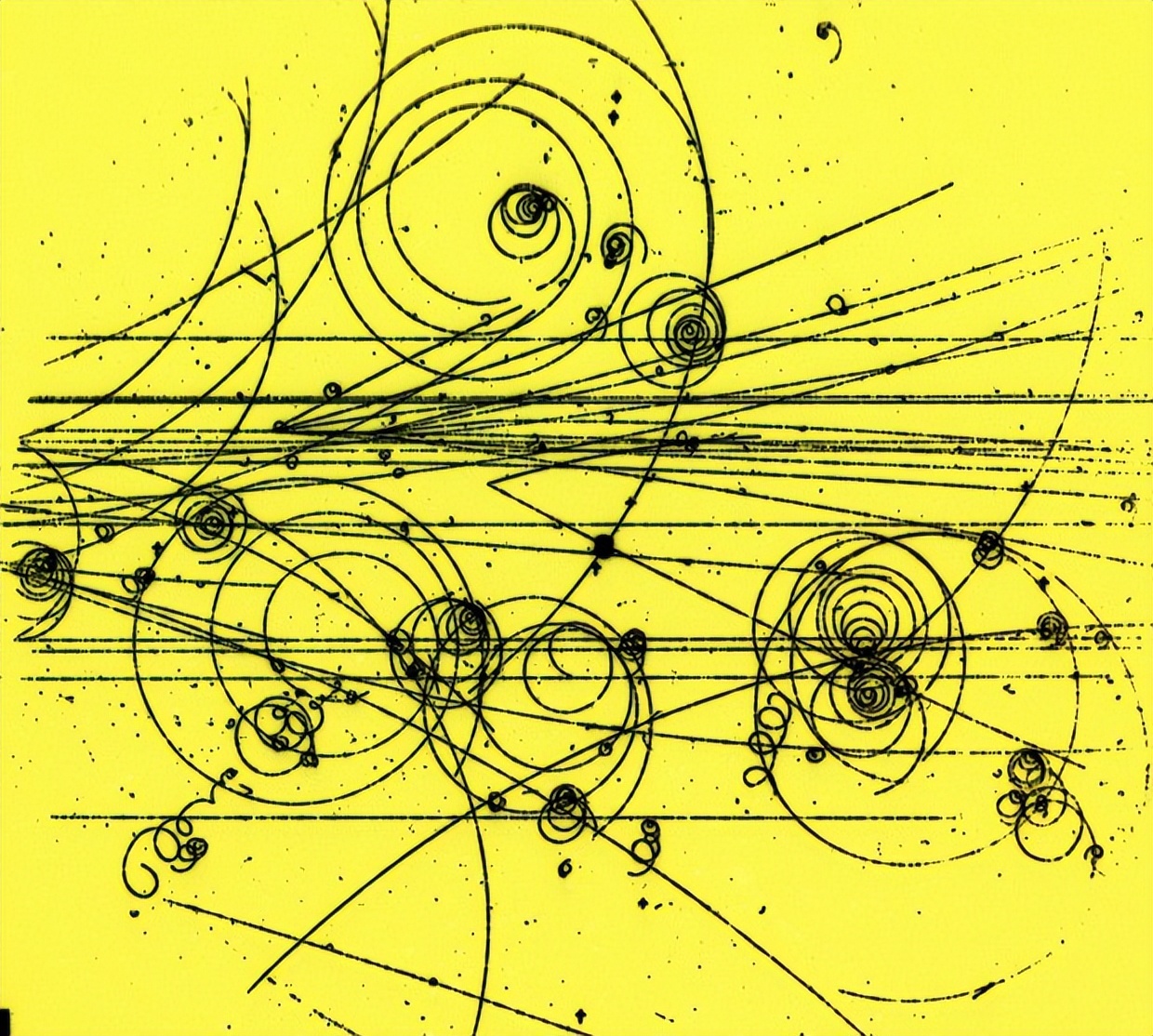
20世纪，在一个最基本的问题上，物理学家取得了巨大的进展。这个问题就是∶构成宇宙万物的基本元素是什么？在这一过程中，他们不得不对某些数学问题的解做出了许多假设。由于这些假设及其推论都有坚实的实验证据支持，科学家对理论的完全正确性十分自信。然而，物理学的飞速进步面临着一个巨大的挑战∶解决物理学背后的数学。杨-米尔斯规范场存在性和质量间隔假设的解决将成为迎接这个挑战的重要一步，并将增加我们对物质本质的理解。这使得这一问题成了人类为理解宇宙而进行的长期探索中最新一步——而这一探索在过去2000年来很大程度上一直依赖数学。
上帝乃几何学家古人相信世界由四种基本元素组成∶土、水、气和火。公元前350年左右，古希腊哲学家柏拉图在他的著作《蒂迈欧篇》中从理论上说明这四种元素都是由微小的固体聚集而成。他论述道，作为物质的基本组块，这四种元素必须有完美的几何形状，也就是使希腊数学家深深着迷的5种正多面体————具有完美对称性的正四面体、立方体、正八面体、正二十面体和正二十面体。

在每个多面体上，每个面都是正多边形，其中所有的边都相等，所有的角都相等。

柏拉图认为，火是由正四面体组成的、土是由立方体组成的、水是正二十面体、气是正八面体。最后一种正多面体代表了整个宇宙的形状。
对于柏拉图而言，上帝必定是一位几何学家。或伽利略说∶为了理解宇宙，你必须先知道描写它的语言。这语言就是数学。
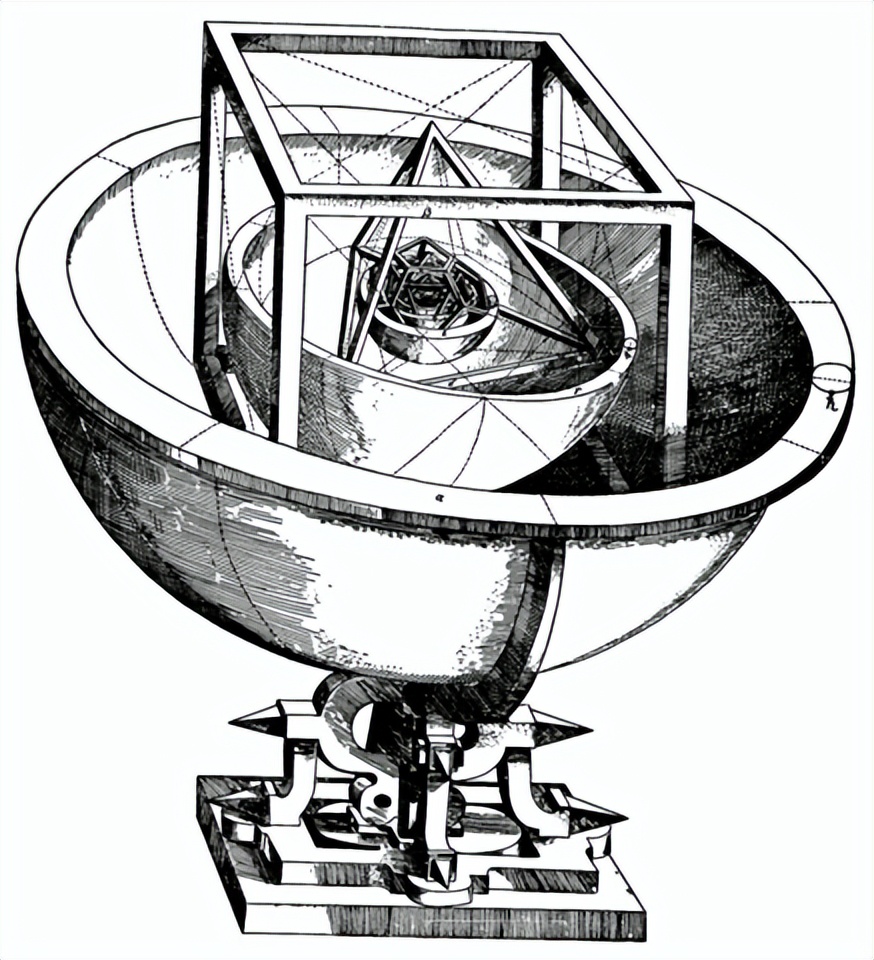
在开普勒生活的时代，有6颗已知的行星∶水星、金星、地球、火星、木星和土星。并且哥白尼已经提出所有这些行星都在以太阳为中心的圆形轨道上运行。开普勒后来证明这些轨道不是圆而是椭圆。开普勒建立了一个理论，用来解释为什么正好有6颗行星以及为什么它们位于离太阳为特定距离的轨道上，这是因为每两条相邻的轨道之间一定是适合正好嵌入一个正多面体，而且每种正多面体正巧使用一次。
经过一些实验后，他终于找到了这些嵌套的正多面体和球面的排列∶最外层球面（土星在其上运动）包含了一个内接立方体，在这立方体内是一个木星轨道所在的内切球面，在这球面内接着一个正四面体，火星在其内切球面上运行。火星轨道所在球面内接着一个正十二面体，而地球运行轨道所在的球面与其内切。地球轨道所在球面又内接着一个正二十面体，而金星运行轨道所在的球面与其内切。最后，与金星运行轨道所在球面内接的是一个正八面体，而水星运行轨道所在的球面与其内切。

这是开普勒自己画的描述其理论的模型。

同柏拉图一样，开普勒也运用了同一基本哲学思想∶宇宙根据数学规律运行。
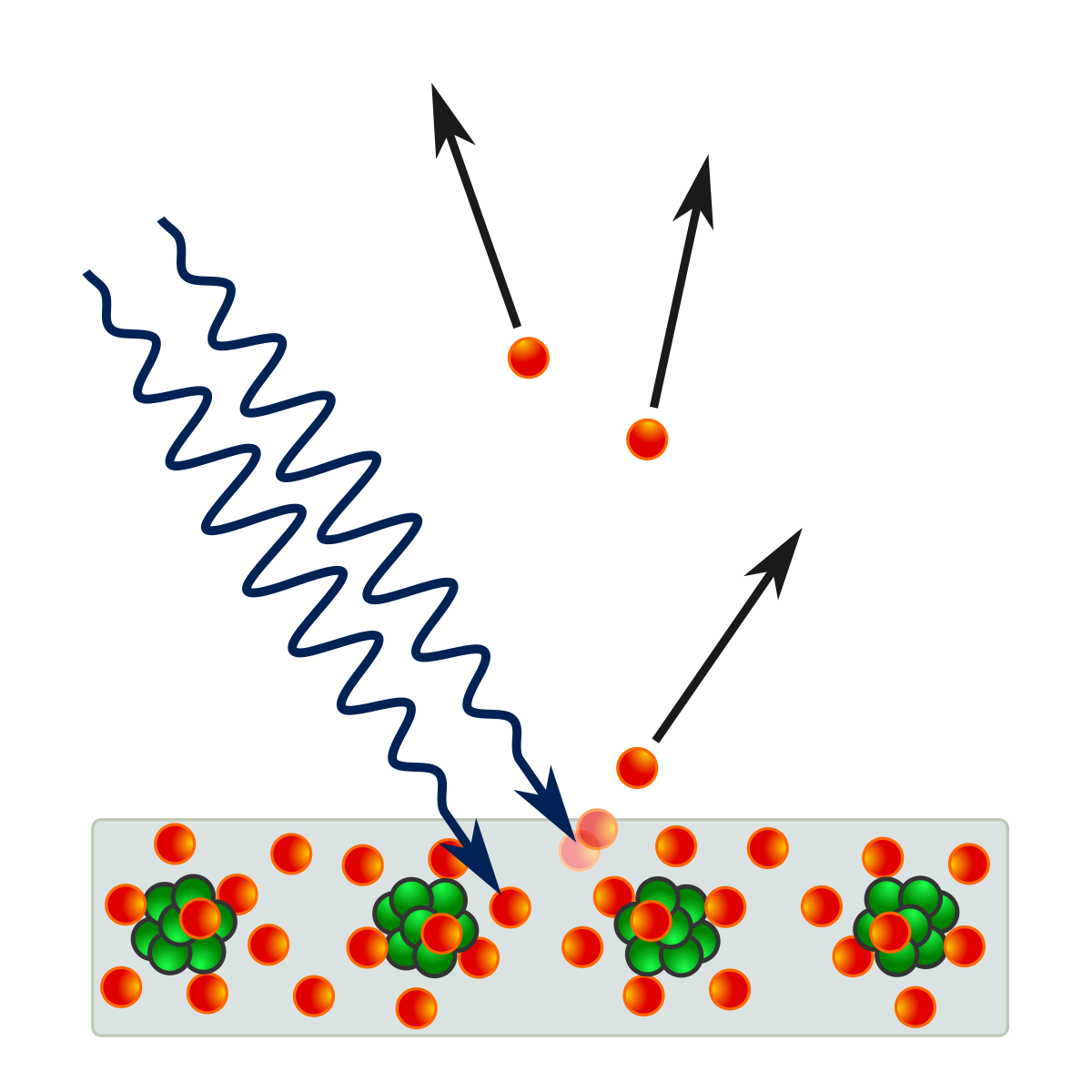
20世纪初，原子论成为被广泛接受的物质理论。它认为一切事物都是由原子构成的，原子好比微型的“太阳系” ，其中一些电子（“行星”）沿某一轨道绕着中心核（“太阳”）运动。
后来，科学家观察到的各种现象迫使他们放弃原子模型。取而代之的是一种更为复杂的数学理论————量子理论。量子理论诞生于20世纪20年代，它包括着这样的思想∶物质中蕴含着内在的不确定性。