回归曲线方程公式相关系数，标准曲线回归方程公式计算器 _曲线

回归曲线方程公式求相关系数

文章插图
回归曲线方程公式求相关系数=∑(Yi-Y平均数)，在直角坐标系中，如果某曲线C上的点与一个二元方程f(x，y)=0的实数解建立了如下的关系：曲线上点的坐标都是这个方程的解，以这个方程的解为坐标的点都是曲线上的点。
微分几何就是利用微积分来研究几何的学科，为了能够应用微积分的知识，我们不能考虑一切曲线，甚至不能考虑连续曲线，因为连续不一定可微。这就要我们考虑可微曲线。但是可微曲线也是不太好的，因为可能存在某些曲线，在某点切线的方向不是确定的，这就使得我们无法从切线开始入手，这就需要我们来研究导数处处不为零的这一类曲线，我们称它们为正则曲线。
标准曲线回归方程公式计算器曲线回归方程公式：y=（a+bx）/x
两个变数间呈现曲线关系的回归，曲线回归是建立不同变量间相关关系的非线性数学模型数量关系式的统计方法。农业化学中各种因素间的相互关系多数是曲线关系。曲线回归分析或非线性回归分析：以最小二乘法分析曲线关系资料在数量变化上的特征和规律的方法。

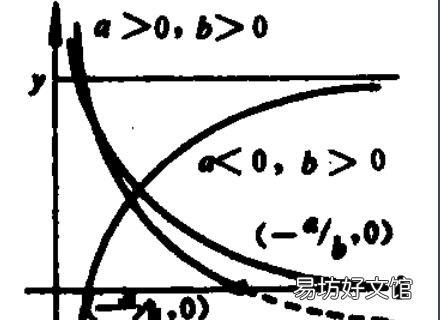
文章插图
扩展资料：
可化为直线的回归是曲线回归中应用最广泛的形式。对某种形式的曲线回归模型取一定形式的变量变换，转换为线性回归模型，即可将曲线回归以线性回归的方法计算出式中各项参数，并进行统计检验和推断。
对等间距水平的试验引进一族正交多项式，经数据变换后符合正交条件，从而消除了各因素之间相关性，并简化计算过程。正交多项式同样适用于多元多项式回归。
回归方程的系数怎么求要求回归方程的系数，可以使用最小二乘法（Least Square Method）。最小二乘法是一种用于求解回归方程系数的方法，它的思想是使用最小化回归方程的误差的平方和的方法求解。
具体来说，最小二乘法的求解过程如下：
首先要确定自变量 x 和解释变量 y 的值。
然后要使用回归方程 y = a + bx 进行拟合，得到回归方程的系数 a 和 b 。
最后要计算回归方程的残差平方和，即回归方程预测值与实际值之差的平方和。
最小二乘法的优点是简单易用，可以很方便地求解回归方程的系数。但是，它对数据的要求比较严格，要求数据是正态分布的，否则它的精度就会受到影响。
线性回归方程中的相关系数r是什么将反映两变量间线性相关关系的统计指标称为相关系数（相关系数的平方称为判定系数）；将反映两变量间曲线相关关系的统计指标称为非线性相关系数、非线性判定系数；将反映多元线性相关关系的统计指标称为复相关系数、复判定系数等。
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标，是研究变量之间线性相关程度的量，一般用字母 r 表示。由于研究对象的不同，相关系数有多种定义方式，较为常用的是皮尔逊相关系数。

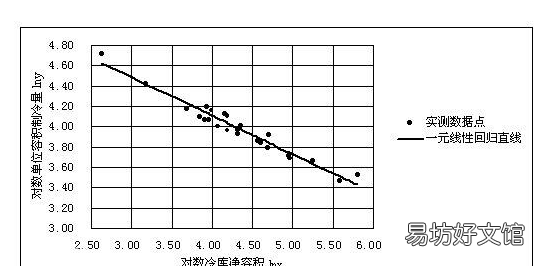
文章插图
扩展资料
样本的简单相关系数一般用r表示，计算公式为：
其中n 为样本量，Xi和X分别为两个变量的观测值和均值。r描述的是两个变量间线性相关强弱的程度。r的取值在-1与+1之间，若r>0，表明两个变量是正相关，即一个变量的值越大，另一个变量的值也会越大；若r<0，表明两个变量是负相关，即一个变量的值越大另一个变量的值反而会越小。
r 的绝对值越大表明相关性越强，要注意的是这里并不存在因果关系。若r=0，表明两个变量间不是线性相关，但有可能是其他方式的相关。
利用样本相关系数推断总体中两个变量是否相关，可以用t 统计量对总体相关系数为0的原假设进行检验。若t 检验显著，则拒绝原假设，即两个变量是线性相关的；若t 检验不显著，则不能拒绝原假设，即两个变量不是线性相关的。
线性回归方程相关系数如何判定相关性的强弱首先我要说,那个东西叫相关系数,不叫相关指数
【回归曲线方程公式相关系数，标准曲线回归方程公式计算器】相关系数r
r=n(写上面)∑i=1(写下面)(Xi-X的平均数)(Yi-Y平均数)/根号下[∑(样子同上)(Xi-X平均数）的平方*∑（样子同上）（Yi-Y平均数）的平方
就是这样了
你能看明白就明白了
不能就算了