两条直线被同一条直线所截,形成了八个角,从位置关系上看可以分为对顶角、邻补角、同位角、内错角、同旁内角,简称为三线八角 。找准这些角的位置关系是计算角度和判断直线位置关系的基础,很多初学者由于对概念理解不透彻,在做题时很容易因位置关系判断判断错误导致题目错误 。
识别两个角是同位角、内错角和同旁内角的前提是:两条直线被同一条直线所截,就是说这几类角只与三条直线有关系,角的两边不可能出现在四条直线上 。所以在判断时,可以先用笔把角的两边画出来,看需要判断的两个角的两边在几条线上 。
其次需要理解透彻这三类角的含义:
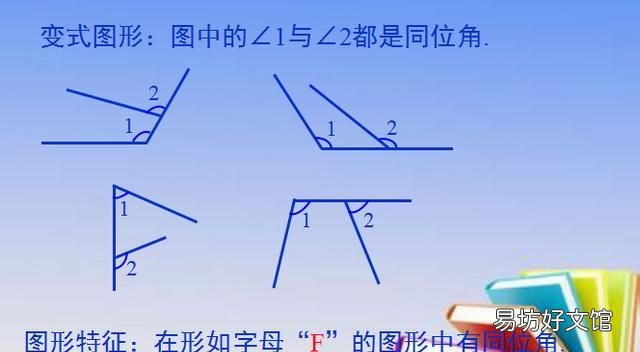
同位角:顾名思义位置相同的角,在截线的同一侧,都在左边或右边,在被截线的同侧,都在上方或下方 。同位角的边所在的直线构成任意旋转的象形字母F状,三线八角中有四组同位角 。
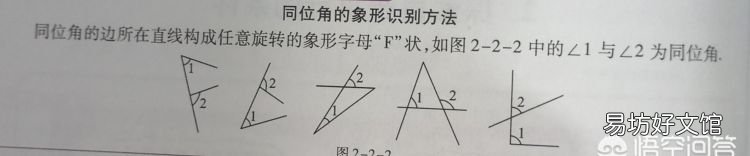
文章插图
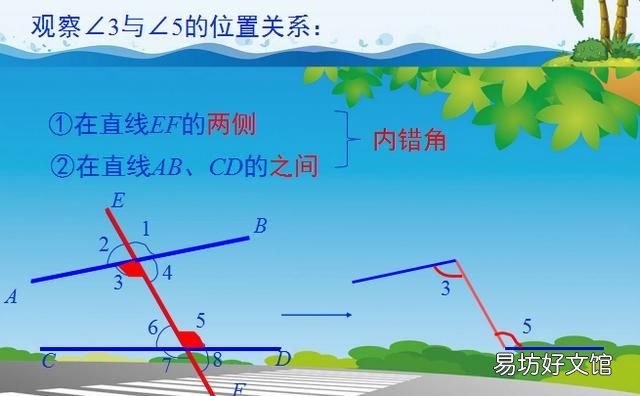
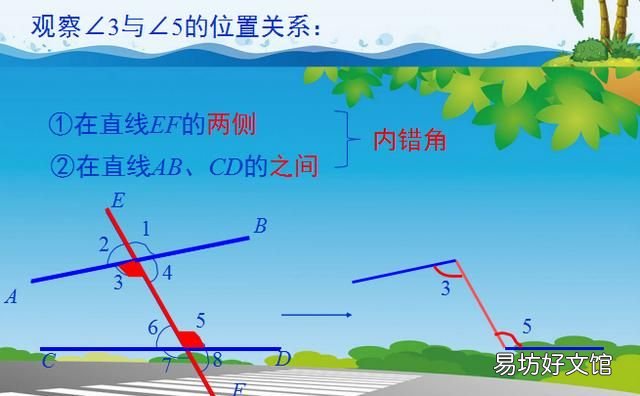
内错角:顾名思义内侧错位的角,具体来说在两条被截直线的内侧,一个角在截线的左侧,那么另一个角就在右侧 。内错角的边所在直线构成任意旋转的象形字母Z状,三线八角中有两组内错角 。

文章插图
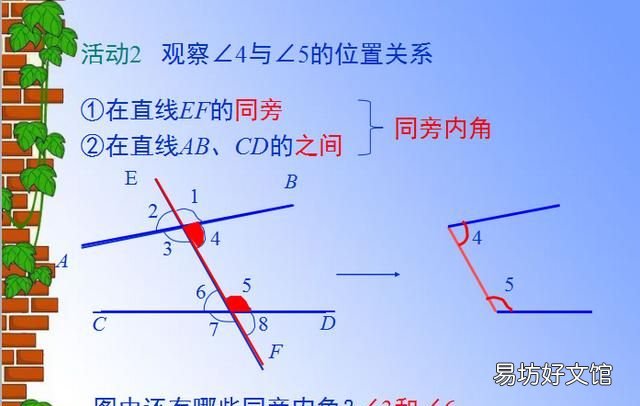
同旁内角:顾名思义内侧同旁的角,具体来说在两条被截直线的内侧,并且在截线的同一侧,要左侧都左侧,要右侧都右侧 。同旁内角的边所在的直线构成任意旋转的象形字母U状,三线八角中有两组同旁内角 。
同位角,内错角,同旁内角,这三类角是在相交线与平行线这章才被引入的新概念 。
平面内两条直线的位置关系有相交和平行两种(重合也就平行了 。)
如果两条直线相交的话,必然会出现邻补角和对顶角 。
领补角相加等于180度,对顶角是相等的 。
两直线垂直是特殊的相交,会产生直角 。
例题一、试判断下图中任意两条直线的位置关系,
【同位角内错角同旁内角】并找出哪些是“领补角”、哪些是“对顶角”和哪些是“直角” 。
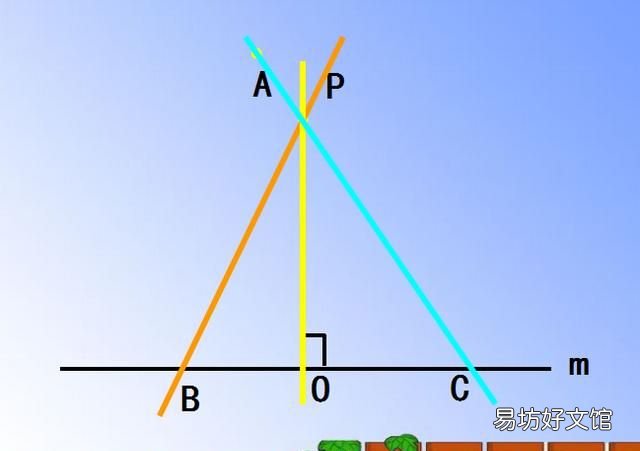
文章插图
通过例题一的学习,我们知道任意两条直线都不平行,如果两条直线平行的话用什么样的条件去判断呢?
这就引入了三类角:“同位角,内错角,同旁内角”,这三类角就是判断平面内两条直线是否平行的条件 。
例题二、
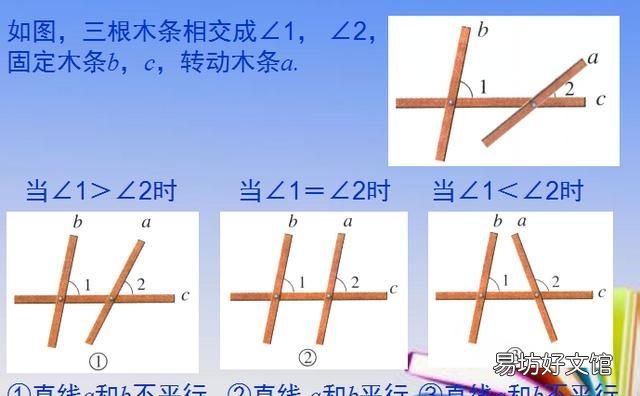
文章插图
1、同位角的概念:
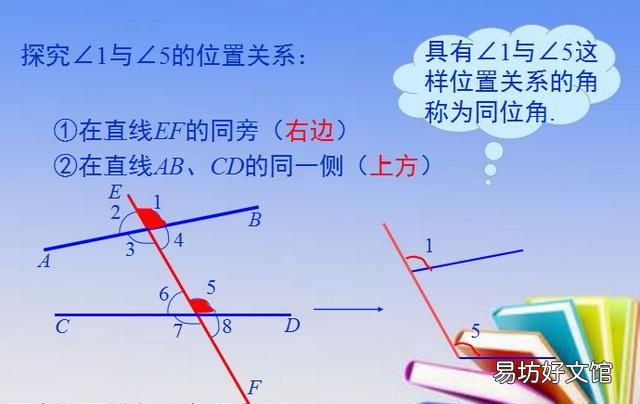
文章插图
如何在具体图形中找到同位角
文章插图
总结归纳

文章插图
2、内错角的概念:
文章插图
如何在具体图形中找到内错角
文章插图
3、同旁内角的概念:
文章插图
如何在具体图形中找到同旁内角

文章插图
总结归纳
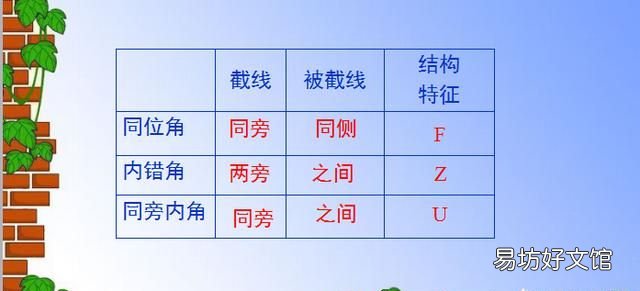
文章插图
最后总结归纳判定两条直线平行的方法:
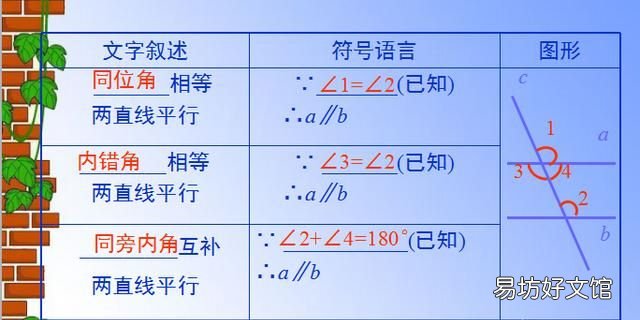
文章插图







