负数减正数，为什么负数乘负数等于正数呢 _正数

进入初中学习有理数运算的时候，就会学习到负数乘以负数等于正数（简称＂负负得正＂），然而无数人跟小编一样，为什么负负得正，限于当时还小自己无法解答问老师也是一样说这是运算规则，你按规则会做题目会运算就行了，当时也只能这样了．想想当时若是深究下去，很可能就是新时代的数学家了．不至于现在还只是一个学霸．，想多了．

文章插图
其实＂负负得正＂是人为设定的，从本质上是不能被证明的，只能被解释，很多人也从数轴及相应的具体事物上可以合理的解释它．为什么负数乘以负数被定义为正数呢，为什么没有被定义为负数呢？当然它不是胡乱设定的，它的设定有其内在规律，下面我们从负数的引入开始解释：

文章插图
负数引入之后（此处省略好多字，负数的引入大家应该都知道），我们必须定义它们的运算规则，使得算术运算能够　保持原来的规律不变，例如我们对负数乘法的定义（－１）（－１）＝１，我们希望保持分配律的不变， a(b+c)=ab+ac结果，如果（－１）（－１）＝－１，就会有（－１）（１－１）＝－２，显然是不符合分配律的，对数学家而言，经过了很长一段时间才认识到＂符合规则＂的负数及分数运算规则是不能加以证明的，它们是我们创造出来的，为的是保持算术基本规律的条件下使运算能够自如．

文章插图
甚至数学家欧拉也常借助一个完全不令人信服的讨论来证明（－１）（－１）必须等于１，因为１（－１）＝－１，如果（－１）（－１）等于－１，那就乱了．
【负数减正数，为什么负数乘负数等于正数呢】有理数是我们创造的，其运算规则如果胡乱的定义，例如分数b/a+c/d=a+b/c+d ，在逻辑上是允许的，但是从度量的观点来看，这无疑是荒谬的；如果这么定义分数的运算规则，那我们的符号算术将变成毫无意义，人们需要创造一个适度的工具，于是思维就顺应了这个要求而自由发挥．

文章插图
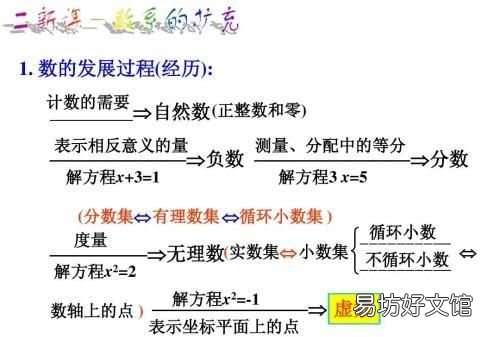
分数、负数等概念存在的纯数意义很明显，因为这种存在扩大了数的范围，方程及有理数的运算都在这个范围内，不会超出这个范围，我们把这个叫做域．直到１９世纪中期，数学家们才完全意识到，在一个扩充的数域的运算，其逻辑和哲学基础本质是形式主义的，于是扩充的数域必须通过定义来创造，这些定义可以是随意的．但是如果在更大的范围内不能保持原来的规则和性质，那扩充的数域将变得毫无意义．故在数学的发展史上，每一次数学危机的产生与解决都离不开数系的扩充，每一次扩充，数的运算规则要么全部延续要么大部分延续，并不会出现任意定义一个新规则．