平行四边形有几个直角，平形四边形有几个角有几个直角 _直角

平行四边形有几个直角

文章插图
平行四边形没有直角，除了特殊平行四边形矩形（长方形）和正方形有四个直角。平行四边形，是在同一个二维平面内，由两组平行线段组成的闭合图形。平行四边形一般用图形名称加四个顶点依次命名。
正方形，是特殊的平行四边形之一。即有一组邻边相等，并且有一个角是直角的平行四边形称为正方形，又称正四边形。正方形，具有矩形和菱形的全部特性。
平形四边形有几个角有几个直角1、平行四边形有四个角，（有一个角为直角的话另外的三个必然为直角）
2、矩形，正方形属于特殊的平行四边形有四个直角，
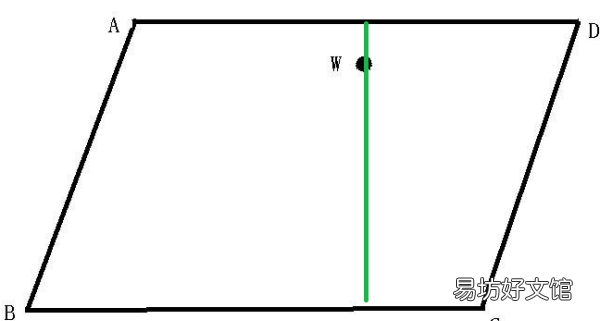
平行四边形有几个直角是矩形【平行四边形有几个直角，平形四边形有几个角有几个直角】平行四边形画一条线段成四个直角如下图：

文章插图
图中线段上面两个直角，下面两个直角，一起四个直角。
扩展资料：
平行四边形与矩形、菱形、正方形：
对于平行四边形而言，矩形独有的性质：四个角都是直角；两条对角线相等且平分（判别直角三角形斜边上的中线等于斜边的一半的依据）。菱形独有的性质：四条边都相等；两条对角线互相垂直，并且每条对角线平分一组对角。而矩形和菱形独有的性质之和就是正方形对于平行四边形独有的性质。
一般地，如果让我们证明一个四边形是矩形或菱形，应先证明四边形为平行四边形，再证明平行四边形是矩形还是菱形。而证明是否是正方形时，我们可以从两个途径着手，和证明矩形、菱形一样，先证明为平行四边形，接着证明是矩形或者菱形，最后通过已知条件或者求证说明是正方形。
平行四边形有几个直角平行四边形没有直角。
如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等。
平行四边形不是轴对称图形，但平行四边形是中心对称图形。矩形和菱形是轴对称图形。注：正方形，矩形以及菱形也是一种特殊的平行四边形，三者具有平行四边形的性质。

文章插图
扩展资料
（1）平行四边形的面积公式：底×高（可运用割补法，推导方法如图）；如用“h”表示高，“a”表示底，“S”表示平行四边形面积，则S平行四边形＝a＊h 。
（2）平行四边形的面积等于两组邻边的积乘以夹角的正弦值；如用“a”“b”表示两组邻边长，α表示两边的夹角，“S”表示平行四边形的面积，则S平行四边形＝ab＊sinα 。
平行四边形有几个直角平行四边形一般没有直角，除了特殊平行四边形矩形（长方形）和正方形有四个直角。