奇数的含义是什么意思，奇数的定义它有什么性质 _含义

奇数的定义它有什么性质

文章插图
1、奇数（odd）指不能被2整除的整数，数学表达形式为：2k+1，奇数可以分为正奇数和负奇数。在整数中，不能被2整除的数叫做奇数。日常生活中，人们通常把正奇数叫做单数，它跟偶数是相对的。
2、两个连续整数中必有一个奇数和一个偶数；奇数+奇数=偶数；偶数+奇数=奇数；偶数+偶数+...+偶数=偶数；奇数-奇数=偶数；偶数-奇数=奇数；奇数-偶数=奇数。
奇数的含义是什么意思【奇数的含义是什么意思，奇数的定义它有什么性质】1、奇数指不能被2整除的整数，数学表达形式为：2k+1，奇数可以分为正奇数和负奇数。
2、在整数中，不能被2整除的数叫做奇数。日常生活中，人们通常把正奇数叫做单数，它跟偶数是相对的。奇数可以分为正奇数和负奇数。奇数的数学表达形式为：
3、奇数与素数是两个不同的概念，奇数可能是素数，也可能不是素数。例如3是奇数，是素数；9是奇数，但不是素数。
质数是什么偶数（也叫双数）：能被2整除的数。如：0 、2 、 4 、 6 、 8 、 10 …………
奇数（也叫单数）：不能被2整除的数。如：1 、3 、 5 、 7 、 9…………
质数（也叫素数）：只有1和本身两个因数的数。如：2 、3、5、7、11、13、17…………
合数：除了1和本身，还有其他因数的数。如：4 、6、8、9、10、12、…………
质数不可再分解，合数可以进一步分解。
扩展资料：
质数的个数是无穷的。欧几里得的《几何原本》中有一个经典的证明。它使用了证明常用的方法：反证法。具体证明如下：假设质数只有有限的n个，从小到大依次排列为p1，p2，……，pn，设N=p1×p2×……×pn，那么，

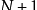
文章插图
是素数或者不是素数。如果

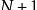
文章插图
为素数，则

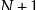
文章插图
要大于p1，p2，……，pn，所以它不在那些假设的素数集合中。
1、如果为合数，因为任何一个合数都可以分解为几个素数的积；而N和N+1的最大公约数是1，所以不可能被p1，p2，……，pn整除，所以该合数分解得到的素因数肯定不在假设的素数集合中。因此无论该数是素数还是合数，都意味着在假设的有限个素数之外还存在着其他素数。所以原先的假设不成立。也就是说，素数有无穷多个。
2、其他数学家给出了一些不同的证明。欧拉利用黎曼函数证明了全部素数的倒数之和是发散的，恩斯特·库默的证明更为简洁，哈里·弗斯滕伯格则用拓扑学加以证明。
合数的一种方法为计算其质因数的个数。一个有两个质因数的合数称为半质数，有三个质因数的合数则称为楔形数。在一些的应用中，亦可以将合数分为有奇数的质因数的合数及有偶数的质因数的合数。对于后者，

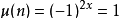
文章插图
（其中μ为默比乌斯函数且''x''为质因数个数的一半），而前者则为

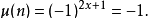
文章插图
注意，对于质数，此函数会传回 -1，且

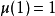
文章插图
。而对于有一个或多个重复质因数的数字''n''，

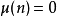
文章插图
。
另一种分类合数的方法为计算其因数的个数。所有的合数都至少有三个因数。一质数的平方数，其因数有

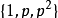
文章插图
。一数若有著比它小的整数都还多的因数，则称此数为高合成数。另外，完全平方数的因数个数为奇数个，而其他的合数则皆为偶数个。
合数可分为奇合数和偶合数，也能基本合数（能被2或3整除的），分阴性合数（6N-1）和阳性合数（6N+1），还能分双因子合数和多因子合数。
数列：1，3，5，7，9，…… ，2n-1，... 称为奇数列，通项公式为

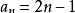
文章插图
。它有一个优美的性质：n取任何正整数时，它的前n项和均是一个完全平方数。
奇数列也可从另一角度进行表述：若

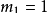
文章插图
，

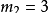
文章插图
，当

文章插图
时，都有

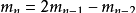
文章插图
，则数列

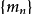
文章插图
为奇数列。
奇数与素数是两个不同的概念，奇数可能是素数，也可能不是素数。例如3是奇数，是素数；9是奇数，但不是素数。
三素数定理：每一个奇数

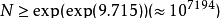
文章插图
都能表示成为三个素数的和。
关于偶数和奇数，有下面的性质：
（1）两个连续整数中必是一个奇数一个偶数；
（2）奇数与奇数的和或差是偶数；偶数与奇数的和或差是奇数；任意多个偶数的和都是偶数；单数个奇数的和是奇数；双数个奇数的和是偶数；
（3）两个奇（偶）数的和或差是偶数；一个偶数与一个奇数的和或差一定是奇数；
（4）除2外所有的正偶数均为合数；
（5）相邻偶数最大公约数为2，最小公倍数为它们乘积的一半；
（6）奇数与奇数的积是奇数；偶数与偶数的积是偶数；奇数与偶数的积是偶数；
（7）偶数的个位一定是0、2、4、6或8；奇数的个位一定是1、3、5、7或9；
（8）任何一个奇数都不等于任何一个偶数；若干个整数的连乘积，如果其中有一个偶数，乘积必然是偶数；
（9）偶数的平方被4整除，奇数的平方被8除余1 。上述性质可通过对奇数和偶数的代数式进行相应运算得出。