合振动方程怎么求

文章插图
1、物理——合振动运动方程求解
两个同方向,同周期的简谐运动方程为x1=4cos(3πt+π/3)和3cos(3πt-π/6),试求它们的合振动的运动方程.)
2、x=x1+x2=Acos(3πt+φ)
A=√4^2+3^2+2*4*3cos[π/3-(-π/6)]=5
tanφ=[4sin(π/3)+3sin(-π/6)]/[4cos(π/3)+3cos(-π/6)]
φ=23°
x=5cos(3πt+23°) 。
两个同方向同频率的简谐振动波的合振动初相怎么求两个同方向同频率的简谐运动,其振动表达式为 x1=6×10^(-2)cos(5t+丌),
x2=2×10^(-2)cos(5t-丌)=2×10^(-2)cos(5t+丌)故合振动x=x1+x2=8×10^(-2)cos(5t+丌)振幅8x10 ^(-2),初相丌

文章插图
扩展资料:
简谐振动波弹簧振子
将一个有孔小球体与一个弹簧连在一起,将一个极为光滑的水平杆穿入小球体,使球体可以在水平杆上左右滑动,而球体与水平杆的摩擦力小得可以忽略不计 。
将弹簧的一端固定住,弹簧的整体质量要比球体质量小得多,这样弹簧本身质量也可以忽略不计 。这个系统便是一个弹簧振子 。
弹簧振子系统在平衡状态下,弹簧没有形变,振子(小球体)在平衡位置保持静止 。若把振子拉过平衡位置,到达最大幅度,再松开,弹簧则会将振子向平衡位置收回 。
在收回的过程中,弹簧的势能转换为振子的动能,势能在降低的同时,动能在增加 。当振子到达平衡位置时,振子所积累的动能又迫使振子越过平衡位置,继续向同样的方向移动 。
但因已越过弹簧振子系统的平衡位置,所以这时弹簧开始对振子向相反方向施加力 。动能转作势能,动能降低,势能上升,直至到达离平衡位置最大幅度的距离 。这时振子所有的动能被转化为势能,振子速度为零,停止运动 。
势能又迫使振子移回平衡位置,在移动过程中,势能转为动能,因而再次越过平衡位置,重复这个过程 。在没有任何其他力影响的完美的条件下,这个弹簧振子系统会在两个最大幅度点间不停地做往返运动 。
弹簧振子的固有周期和固有频率与弹簧弹力系数和振子质量有关,与振幅大小无关
简谐振动的运动学方程D对 。
两个分运动的位移的矢量和,等于合运动的位移 。
X=X1+X2
如果从纯数学角度算,就是X=2*10^(-2)*[ cos(10 t +π/3)+ cos(10 t -π/3) ]
=2*10^(-2)*{ 2*cos[ 《(10 t +π/3)+(10 t -π/3)》/ 2 ]*cos[ 《(10 t +π/3)-(10 t -π/3) ]》/ 2 }
=2*10^(-2)*[ 2*cos( 10 t )*cos(π/3) ]
=2*10^(-2)*cos( 10 t )
如果从物理的角度看,这两个分位移是模相等、初相分别为(π/3)和(-π/3),即它们初相差为(2π/3),是120度,所以它们的合成,结果的模不变,而初相为0了 。
大学物理1.x=λ/4处介质质点的合振动方程
把 x=λ/4 分别代入两个波动方程,得两个振动方程为:
y1 = Acos(2πνt - π/4) 和 y2 = 2Acos(2πνt + π/4)
用旋转矢量图法很容易得到,合振动的振幅为 A,初相位 π/4,所以合振动方程为:
y = y1 + y2 = Ac紶花官拘擢饺规邪海矛os(2πνt + π/4)
2.x=λ/4处介质质点的速度表达式
v = - 2πνAsin(2πνt + π/4)
大学物理振动的合成需要满足一定的条件,题目中的频率相等,合成方法如下:
1、先写出振动分量x1的方程其振动角速度为w;
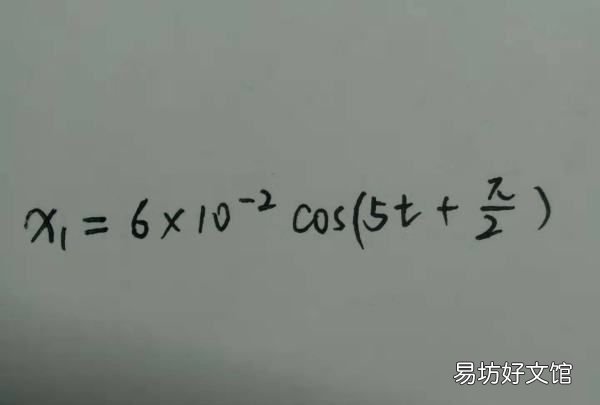
文章插图
2、再写出振动分量x2的方程,应根据余弦函数的对称性将其化成振动角速度为w的振动分量;

文章插图
3、观察两个振动分量,分别写出两个分量的初相角和振幅;
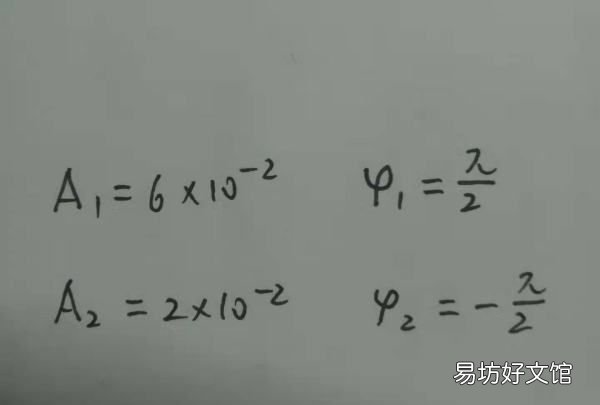
文章插图
4、按照合成公式带入相应的数,可以得到合成振动的振幅为0.02;

文章插图
5、按照合成振动初相角公式带入数目,得到初相角的余切值为无穷,应取角度为90度 。

文章插图
【合振动方程怎么,两个同方向同频率的简谐振动波的合振动初相怎么求】
推荐阅读
- 牡丹喜欢什么土 适合的土嚷盘点
- 铝合金表面腐蚀是什么原因造成的
- 适合90后发朋友圈的句子 吸引90后点赞的精致说说
- 离合器原理,摩擦离合器的工作原理是什么
- C1科三多少分合格
- 2022姓王虎年出生男孩子名字 适合属虎宝宝起名宜选字
- 百合种球适合在夏季种植么 百合种球夏天可以种植吗
- 根据我国法律规定网贷中介合法吗
- 合同倒签合法吗
- 深蓝射频适合多大年龄







