拉格朗 拉格朗日方程与哈密顿原理,终极的自然原则,宇宙的主要动力
文章插图
拉莫尔(英国物理学家和数学家,在对电,动力学,热力学和物质电子理论的理解方面进行了创新)对最小作用原理有一种强烈的、近乎神秘的忠诚……对他来说,这是终极的自然原则——宇宙的主要动力。——阿瑟·爱丁顿
两个粒子具有质量M?和M?,在半径为R的环形上无摩擦滑动。两个质点通过弹簧上的圆弧A连接起来,圆弧A的弹簧系数是k?,自然长度是 a? ;圆弧B的弹簧系数是k?,自然长度是a?。弹簧平放在桌子上。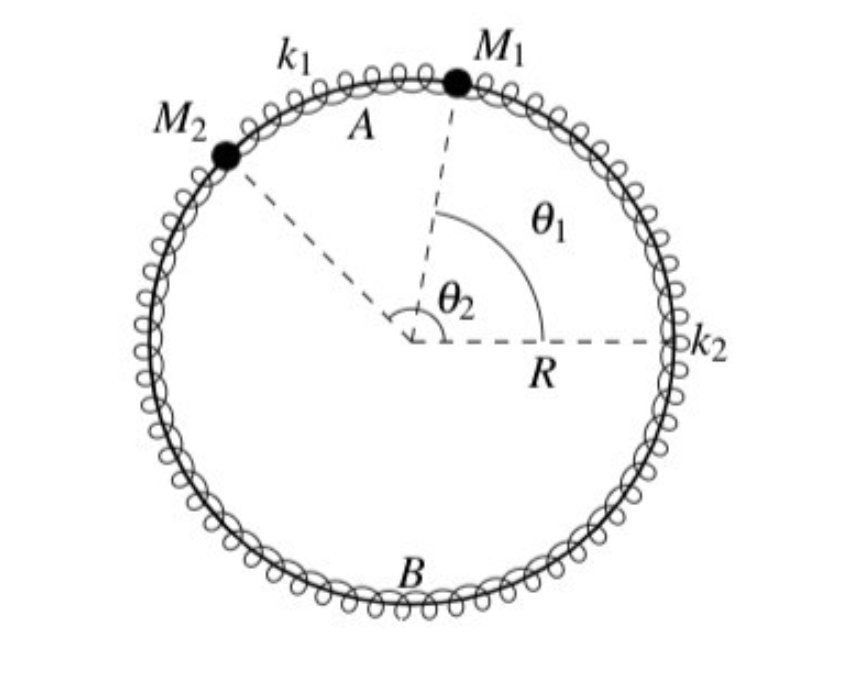
文章插图
假设要求我们找出质点的运动方程。原则上,牛顿的运动定律足以解决这个问题。但在实践中,用牛顿定律为一个复杂的系统寻找运动方程是困难的。即使这个问题与现实世界中机械系统的复杂性相比也显得微不足道。
当我们发现一个问题太难时,一个好的处理方法是尝试改变我们对这个问题的看法。但我们应该采用什么样的新视角呢?
我们从光学研究中得到了一个令人惊讶的答案。
费马最短时间原理反射光的基本定律自古以来就已为人所知。当一束光入射到反射面上时,入射角等于反射角: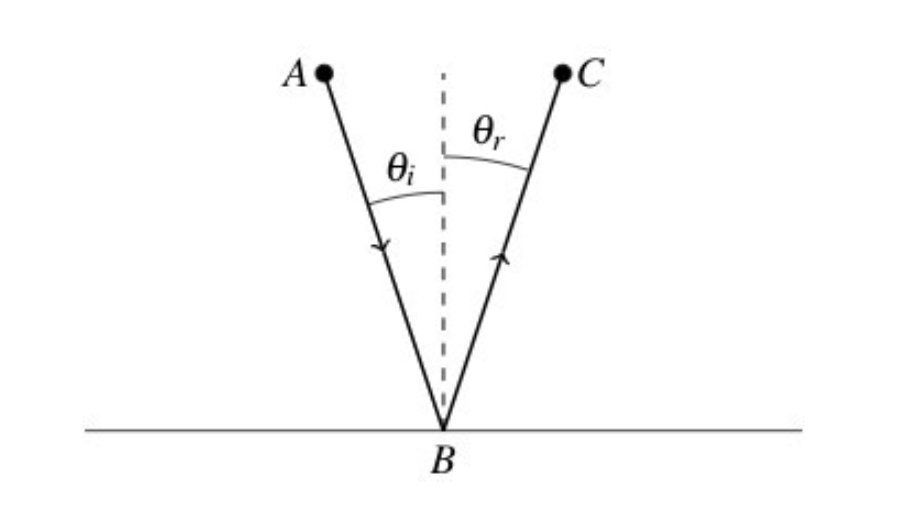
文章插图
亚历山大港的希罗(希腊数学家和工程师)能够从这个事实证明光线所走的路径是它从源头、镜子到目的地的最短路径。也就是说,给定点A和C,光线在点B从镜子上反射,使得路径的长度最小。
古人无法解决的是折射的问题。当一束光入射到分离两种不同物质(典型的例子是空气和水)的表面时,光线会发生弯曲。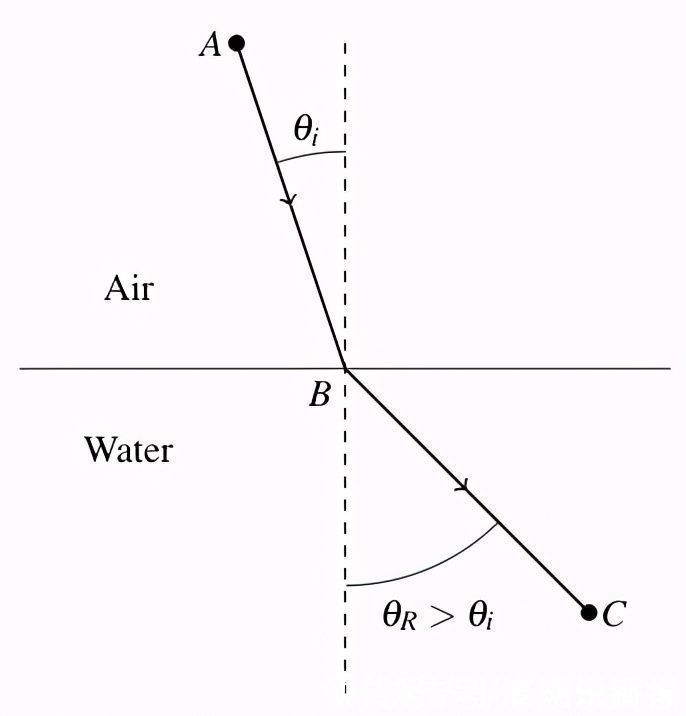
文章插图
离开A点的一束光,到达B点的水面,最终到达C点,并不是走A点和C点之间最短的路径。
有关入射角和折射的定律被称为斯涅尔定律,以威勒博德·斯涅利乌斯(1580-1626)命名,尽管它最早是由伊本·萨尔在公元984年发现的。它指出: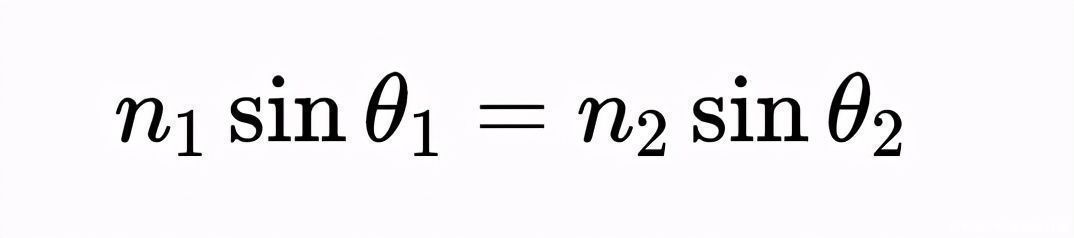
文章插图
其中n是每种介质的折射率。这一定律是实验发现的,缺乏理论论证。皮埃尔·德·费马(1607-1665)提出了一个证明。费马扩展了古希腊人的发现(即反射光在两点之间的路径最短),取而代之的是光选择了两点之间最短时间的路径。从这个公设,他可以推导出斯涅尔定律。这是中级物理教科书中常见的练习,我可能会在一篇简短的后续文章中讨论它。
费马原理被认为是历史上第一个重要物理思想的例子,自然界将设法以这样一种方式进行物理过程,以尽量减少这一过程所需要的一些重要的量。当然,这里没有任何超自然现象发生,这个观点在19世纪就有了坚实的科学基础。在本文的剩余部分,我们将通过拉格朗日形式主义理论来探讨这一观点。
约束条件,广义坐标和构型空间我们总是可以用笛卡尔坐标(x,y,z)来表示系统的状态,但根据问题的不同,我们可以选择更有用的变量。我们甚至可以减少我们需要考虑的变量的数量。例如,球面上的点P可以完全用极角和方位角(θ,φ)来表示,如下图所示: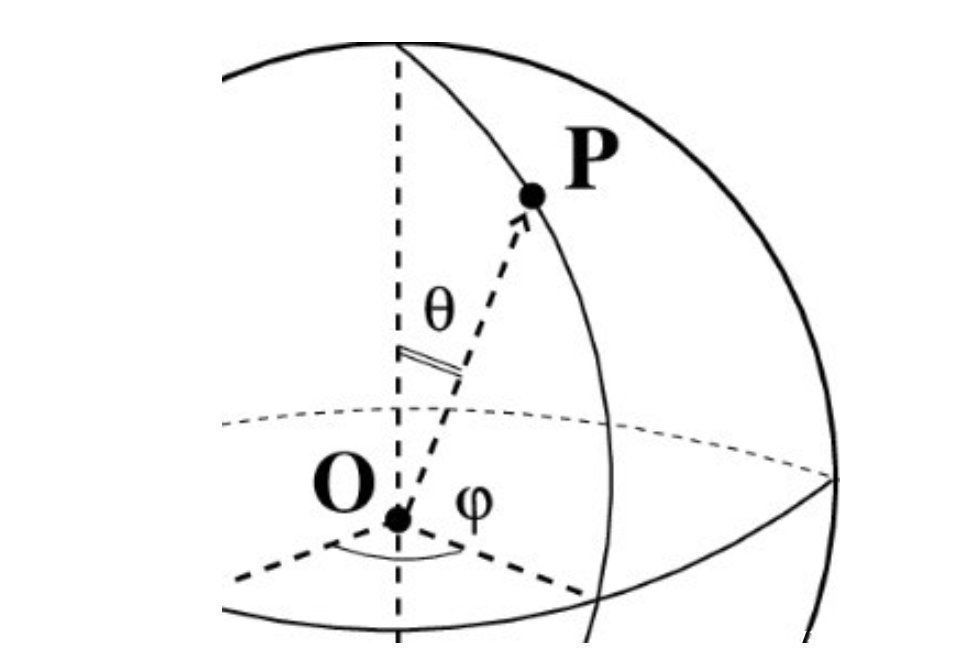
文章插图
任意变量q?,q?, …,q?被称为广义坐标。广义上说,它们可以是我们想要的任何东西,只要它们完全指定了系统的状态而且它们之间没有任何函数依赖性。广义坐标的时间导数称为广义速度。知道应该使用哪些变量是一种直觉技能,只有通过实践才能学会。
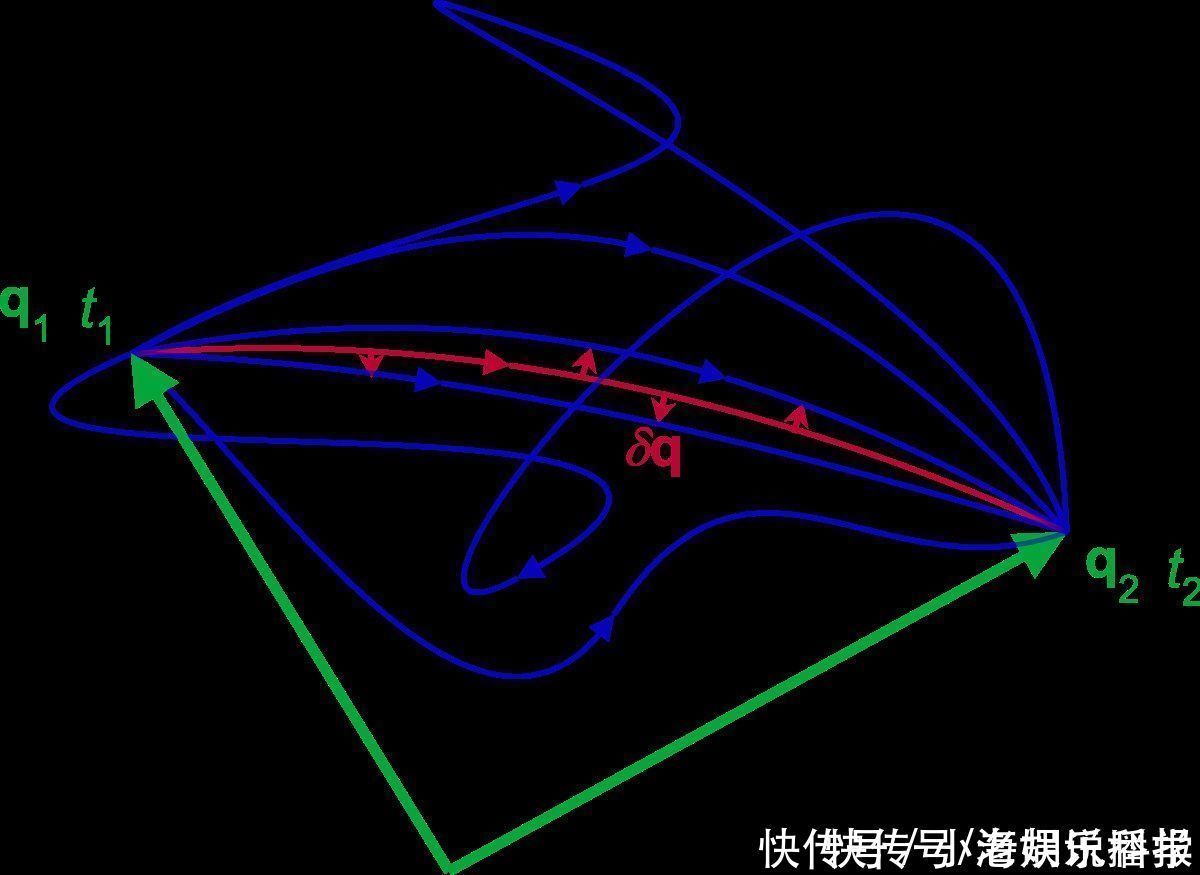
当我们选择了广义坐标,我们就可以把系统在任意时刻的状态表示为构型空间中的一点。随着时间的推移,系统在构型空间中跟踪的路径称为轨迹。
文章插图
一个机械系统随时间的演化的问题,可以通过看系统在构型空间遵循哪个轨迹来解决。
插曲:泛函假设一束光在点A和点B之间沿(x,f(x))给定的平面内路径传播:
文章插图
设v(x)为光速与x的函数,在折射率为n的介质中,v=c/n。在这个问题中,n是y的函数,有:
推荐阅读
- 结婚纪念日当天怎么过 结婚纪念日怎么算
- 为什么日漫的结局大多让人累觉不爱
- 柠檬日是什么意思
- 如何评价正在播放的由庵野秀明主导的日本动画人博览会
- 苹果Safari涉嫌侵犯专利遭起诉
- 糖尿病日是哪天
- 诺贝尔瓷砖价格表图片 诺贝尔瓷砖怎么样
- 夏侯渊之死 夏侯??怎么死的
- 惠达卫浴54—A51E 惠达卫浴怎么样
- 艾瑞泽7混动版怎么样 艾瑞泽7怎么样







