拉格朗 拉格朗日方程与哈密顿原理,终极的自然原则,宇宙的主要动力( 三 )
文章插图
现在我们考虑T对广义速度的导数。按照上述推理:
该量的时间导数为: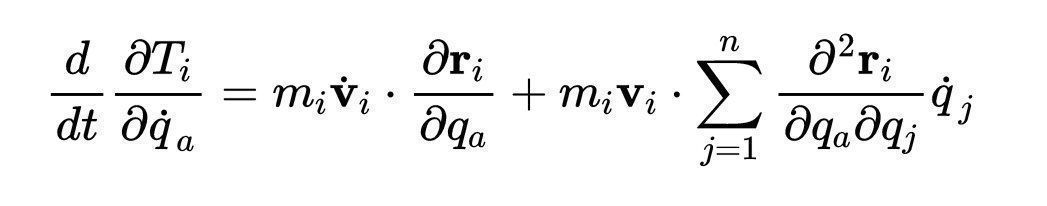
文章插图
通过对所有N个粒子求和,我们发现: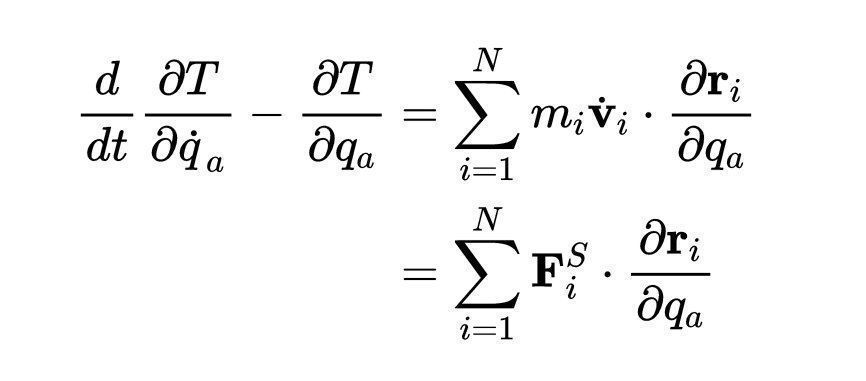
文章插图
上标S的F表示作用在第i个粒子上的牛顿力是广义坐标的函数。现在我来完成这个证明,证明这个和等于广义力F?。
设A、B为构型空间中的两个“位置”,它们由一条平行于q?轴的直线相连。对于两个自由度的情况,这看起来像: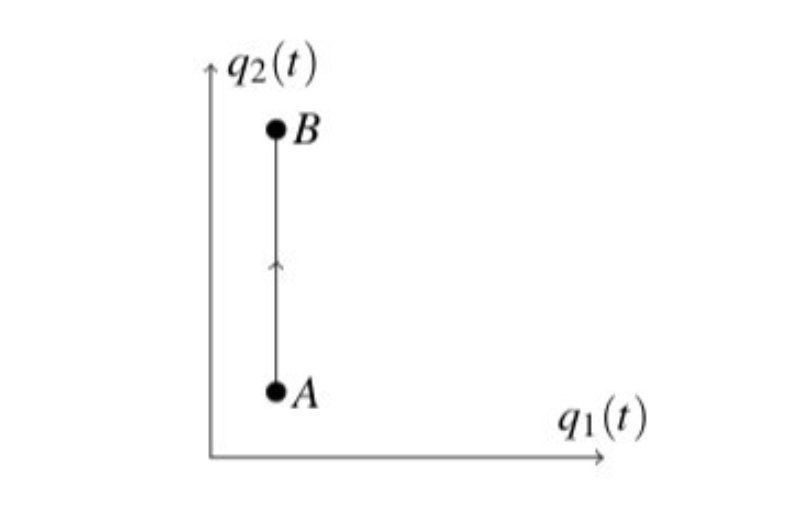
文章插图
这个量从A到B的线积分是:
右边的线积分是第i个粒子q?从A到B的位置向量所经过的每条路径C_i上的线积分,根据定义,这是系统A和B之间的势能差的负值: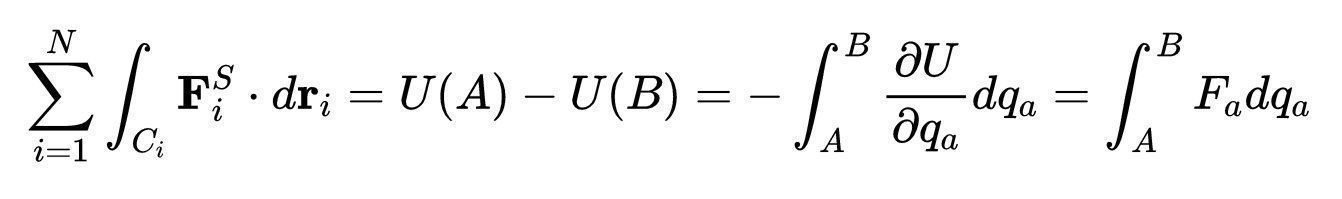
文章插图
- 中间等式是由微积分基本定理提出的。
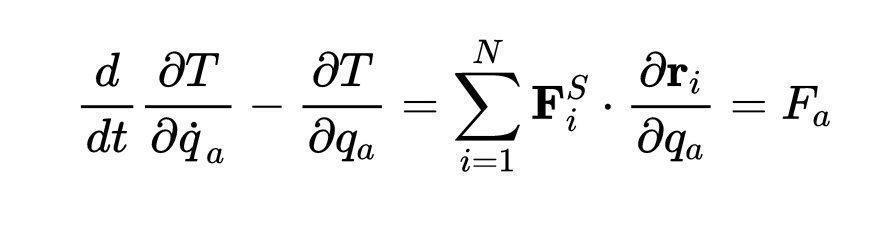
文章插图
这让我们完成了证明:
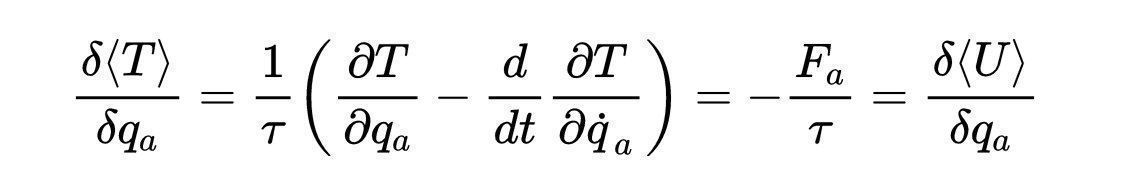
文章插图
这意味着,对于真实轨迹的变化,我们有:
这个积分叫做作用泛函。我们所做的就是证明哈密顿最小作用量原理,即机械系统在构型空间中的运动轨迹是使作用泛函最小的轨迹。
函数L=T-U非常重要,它有自己的名字,被称为拉格朗日方程。我们得到欧拉-拉格朗日方程:
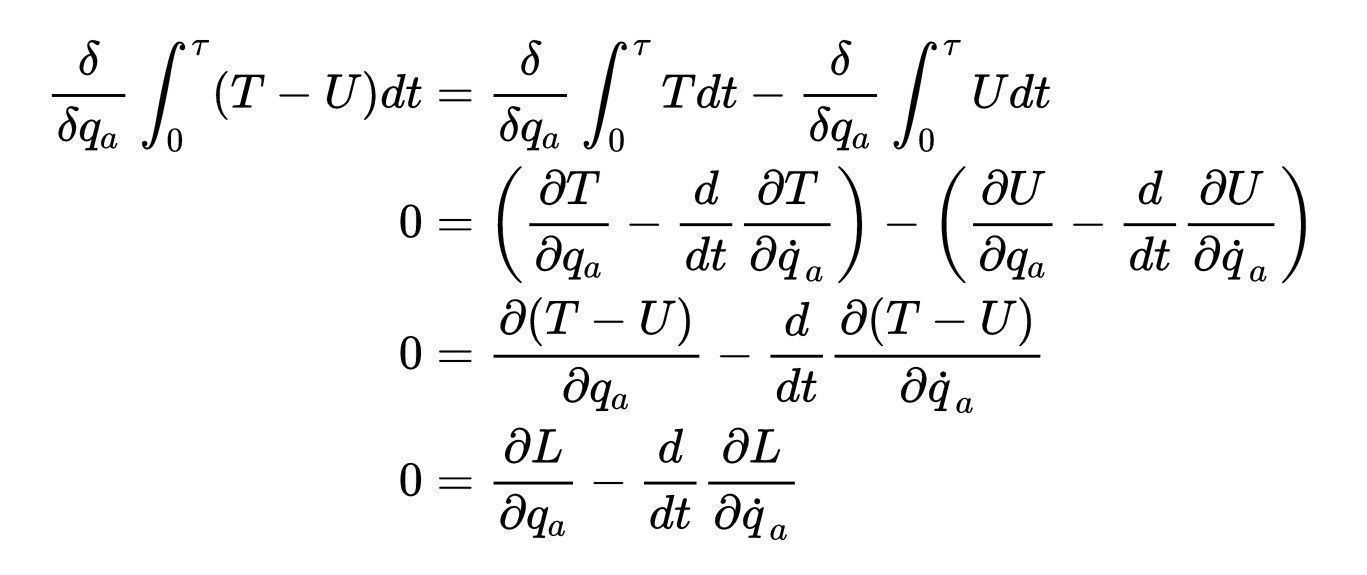
文章插图
欧拉-拉格朗日方程给出了每个q?的运动方程。对于很多重要的机械系统来说,一旦你有了拉格朗日方程,找到运动方程就很简单了。我们可以说,关于标准系统状态随时间演化的所有信息都包含在拉格朗日量中。
什么时候拉格朗日方法有效?许多重要的力学问题涉及沿固定表面或路径的运动。例如,如果一个质点在球面上移动,那么它的位置坐标(x,y,z)满足x2+y2+z2-R2=0。可以用f(x,y,z)=0的形式表示的约束称为几何约束。
我们也可以有一个运动约束。正如几何约束限制了粒子的位置一样,运动约束限制了粒子的速度。例如,如果我们说一个粒子的速度完全在x方向上,那么这是一个运动学约束,速度的y和z分量为零。积分之后,这个运动约束变成了一个几何约束,它表示位置的y和z分量是常数。当这是可能的,我们说运动约束是可积的。
拉格朗日方程只适用于只有几何和可积运动学约束的系统。我们称这样的系统为完整系统。一类重要的非完整约束的例子是:例如,如果一个球在桌子上,并被一根长度为l的绳子拴在原点上,那么约束是x2+y2≤l2。
拉格朗日力学对于保守力总是有效的。有时它可以扩展到非保守力,但这并不总是一个好方法。虽然这听起来像是一个弱点,但事实证明,保守的完整系统是非常庞大的,包含了人们可能会遇到的大多数有趣的问题。
说了这么多,我们来看一些例子看看拉格朗日形式主义的实际应用。
一个钟摆
一个质量m附着在一个长度为l的刚性轻棒的末端,并产生小角度的振荡。

文章插图
当运动是二维的时候,运动完全可以用角θ来表示。从笛卡尔坐标开始,然后进行转换通常是个好方法。动能为:
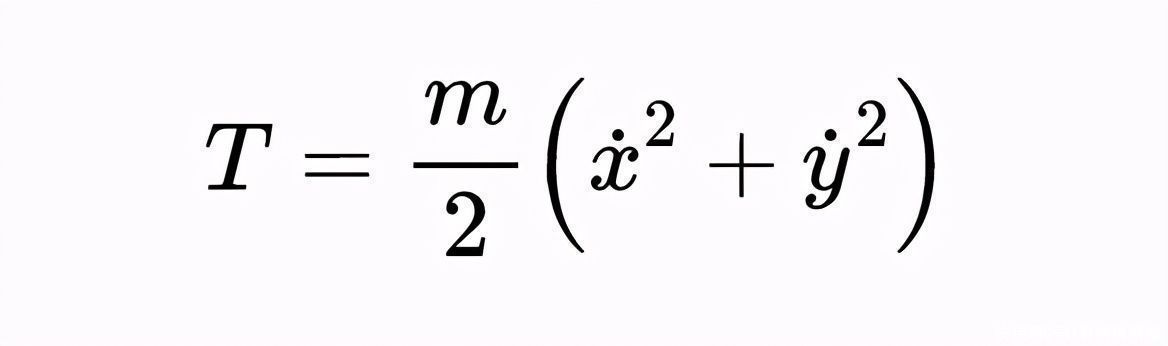
文章插图
重力势U=mgy。因此:

文章插图
然后我们用x=lsinθ, y = lcosθ来求广义坐标θ下的L,用链式法则计算x导和y导:
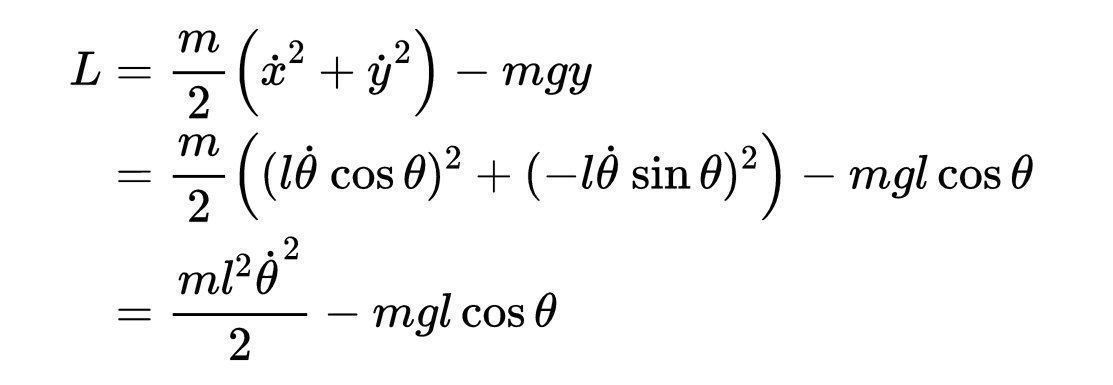
文章插图
【 拉格朗|拉格朗日方程与哈密顿原理,终极的自然原则,宇宙的主要动力】那么θ的拉格朗日运动方程为:
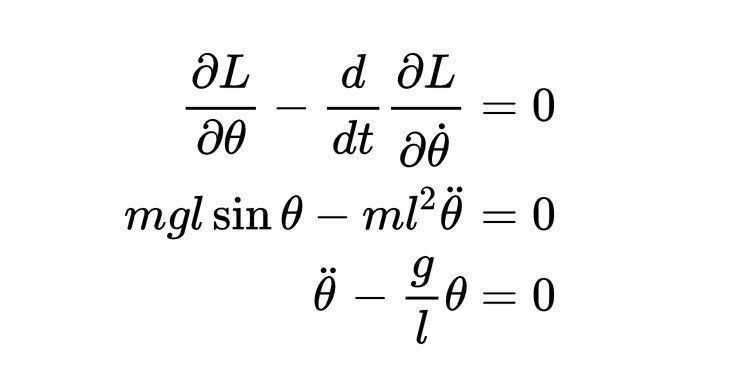
文章插图
- Sinθ≈θ对于小θ
质量为M的物体在一个方向上来回运动。木块附着在两个相同的弹簧上,弹簧常数为k,自然长度为a。弹簧固定在墙上,x=±a。

推荐阅读
- 结婚纪念日当天怎么过 结婚纪念日怎么算
- 为什么日漫的结局大多让人累觉不爱
- 柠檬日是什么意思
- 如何评价正在播放的由庵野秀明主导的日本动画人博览会
- 苹果Safari涉嫌侵犯专利遭起诉
- 糖尿病日是哪天
- 诺贝尔瓷砖价格表图片 诺贝尔瓷砖怎么样
- 夏侯渊之死 夏侯??怎么死的
- 惠达卫浴54—A51E 惠达卫浴怎么样
- 艾瑞泽7混动版怎么样 艾瑞泽7怎么样







