定义|大数定律-----概率论正式化的重要一步表达式|定律|硬币|变量|差异

文章图片

一个常见的直觉是，进行更多次的实验会得出更准确的结果。这种直觉被称为大数定律。然而，这并不是常识。为什么我们学会了这种思考方式？我们又如何知道它是真的呢？
这个概念首先由杰罗拉莫-卡达诺（ Gerolamo Cardano）提出，他也因成为第一个认识负数的数学家而闻名。虽然他说统计学的准确性倾向于随着试验次数的增加而增加，但他从未证明这一理论。这一直觉慢慢被各种数学家证明和扩展，包括雅各布-伯努利、泊松、切比雪夫、马尔科夫等人。
大数定律是概率论正式化的第一个重要步骤之一。证明这一定律有赖于一些符号的发明。此后，它被分成两个版本：弱和强。
在本文中，我将讨论伯努利对二元变量使用的原始版本。二元变量是指只能有两个值的变量，如抛硬币。另一个常见的例子是从一个装有黑球和白球的罐子里取球（每次取完后我们都把球放回罐子里，这样概率就不会改变）。
当我们研究二元分布时，通常将一个事件设为1 ，概率为p ，将另一个事件设为0 ，概率为1-p 。对于抛硬币，我们可以将正面设为1 ，概率p = 0.5 。
再定义几个术语，然后我们就可以开始分析这种情况了。假设我们取了一个大小为n的样本（抛掷硬币n次）。如果我们把样本中每个元素的数量加起来，然后除以n ，就可以得到我们的样本平均值，我们将其定义为μ(n) 。
举个简单的例子，如果我们扔了10次硬币，得到4个正面（所以6个反面），那么μ（n）=0.4 。每次我们取样， μ(n)都可能发生变化，因为这是一个非确定性的过程。
还有一个简单的术语需要定义！当我们取P（事件）时，这相当于该事件的概率。所以P（证明朝上）=0.5 。
让我们直观地想一想大数定律对这种情况是怎么说的。当n（掷硬币的次数）变大时，我们期望μ（n）（样本平均值）接近p（0.5）。这是非常直接的，但我们如何正式说明这一直觉呢？
请注意，这句话并没有说到证明朝上的绝对数量，只是说到证明朝上相对于总掷硬币的数量。奇怪的是，当n变大时，我们预计正面和反面数量的绝对差异会随着sqrt(n)的增长而增长。
现在我们正式定义弱大数定律。对于二元变量，弱大数法则是这样的。对于任何ε>0 。

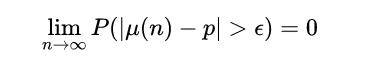
文章图片

二元变量的弱大数定律
这个表达式的符号很重，但我们可以把它分解。前面的极限只是表达了 "大数 "的部分：我们采取了一个非常大的样本量。我们有一个表达式P(f)=0的事实，意味着f没有发生的机会。我们这里的f是|μ(n)-p|>ε 。由于ε>0并且我们有绝对值， f没有发生的机会这一事实意味着μ(n)和p之间的差异不会超过ε 。

定义|大数定律-----概率论正式化的重要一步

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)