作者: 伯克利人工智能实验室(BAIR)三年级博士生 董镇
NeurIPS 2020 文章专题
第·12·期
混合精度量化 (Mixed-Precision Quantization) 是模型压缩领域的重要方法 。 HAWQ(音同Hawk , 鹰) 提出了一种基于Hessian矩阵的可以全自动确定混合精度的方法 。 其核心思想是使用敏感度分析 , 对神经网络中特别敏感的层使用高量化位宽 , 对不敏感的层使用低量化位宽 。
本文是伯克利人工智能实验室 (BAIR)发表于 NeurIPS 2020的一项工作 , 提出Hessian矩阵的迹是衡量敏感程度的重要指标 , 并且基于此进行了组合优化 。HAWQ的方法在不同模型和不同任务上泛化很好 , 取得了SOTA的量化结果
(ImageNet Top1:8MB ResNet50 75.9% , 1MB SqueezeNext 68.7%)。

文章图片
视频简介:
相关代码:
https://github.com/Zhen-Dong/HAWQ
一、问题描述
边缘计算由于其低延迟、低成本、低功耗、隐私保护等优点在近年被广泛研究 。 量化 (Quantization) 又称定点化方法 , 是模型压缩的重要分支 , 对于生成高效的神经网络模型 , 赋能边缘计算 , 有着重要意义 。 但是在超低位宽 (高压缩率) 的情况下使用统一的量化比特数 (位宽) 会严重影响模型的表现 。 混合精度量化允许神经网络的每一层拥有不同的量化位宽 , 从而可以很大程度上保留模型的精确度 , 但是确定每一层的位宽导致了一个指数级的搜索空间 。 已有工作使用强化学习或者可微分搜索等方法来确定每一层的量化位宽 , 但因为每搜索一步就要量化一个神经网络来得到反馈 (量化一个神经网络的开销和训练一个神经网络的开销在一个量级), 使得已有算法很耗时且对计算资源十分依赖 。
二、方 法
本文提出了一种基于敏感度分析的方法来确定每层的量化位宽 。 神经网络中不同的层有着不同的作用 , 相对应的 , 对最终模型预测结果的影响也不尽相同 。
文章图片
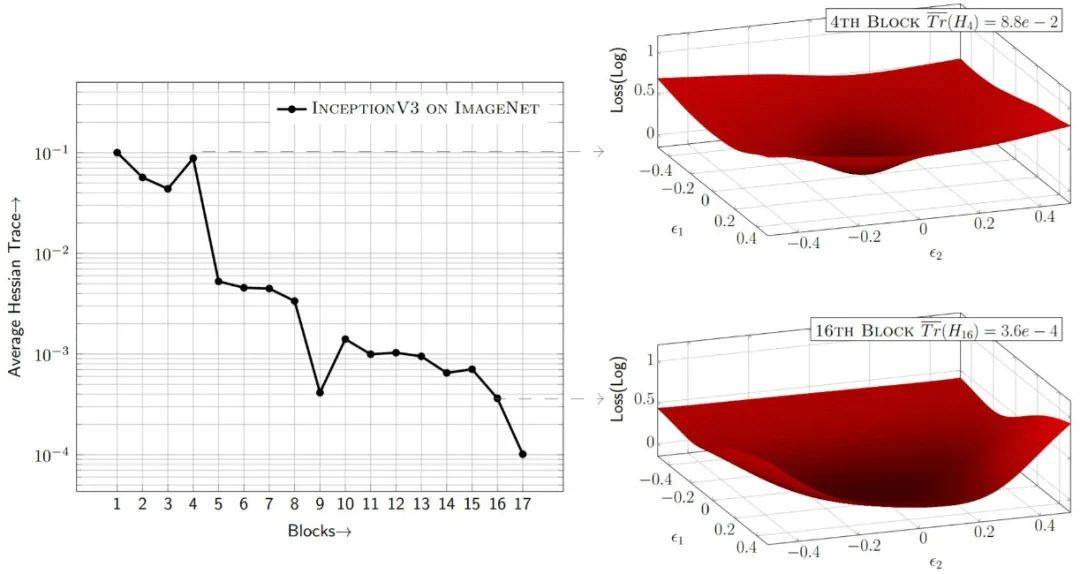
如图所示 , 本文作者对预训练模型中某一层的权重进行干扰 , 而保持其他层的权重不变 。 为了可视化 , 权重干扰方向为最大的两个Eigenvector对应方向 (在任意的两个方向施加微小扰动只会对loss产生不可见的微扰 , 所以选用Eigenvectors), 对每个干扰计算loss就得到了图中的损失函数图像loss landscape 。 可以看到 , 对于InceptionV3而言 , 其第4个block (为了可视化可以把神经网络几层合并为一个block) 的loss landscape很陡峭 , 说明对于干扰比较敏感 , 但是其第16个block的loss landscape却很平缓 , 说明对于干扰不敏感 。 基于此可以给敏感的第4个block更高的量化位宽 , 而给不敏感的第16个block较低的量化位宽 。
以上画出loss landscape做判断的方法开销很大 , 实际操作时需要用敏感度作为判断依据 。 HAWQV2假设预训练的模型已经收敛 , 因此文章中忽略一阶影响而使用二阶分析 (Hessian) 来判定模型的敏感度 (量化过程要使用量化模拟来再训练模型 , 所以衡量敏感度比损失函数变化值本身更为重要)。 本文从数学上证明了Hessian矩阵的迹除以权重数量 (等价于eigenvalues的平均值 , 后文简称为平均迹) 可以作为衡量敏感度的标准 。 图中第4个block的Hessian矩阵的平均迹是8.8e-2 , 而第16个block的Hessian矩阵的平均迹是3.6e-4 , 对应的第4个block比第16个block敏感很多 。
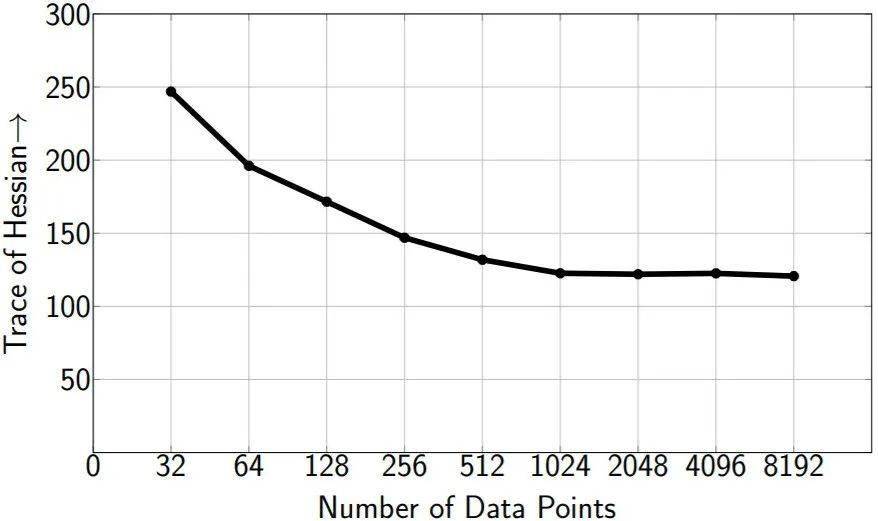
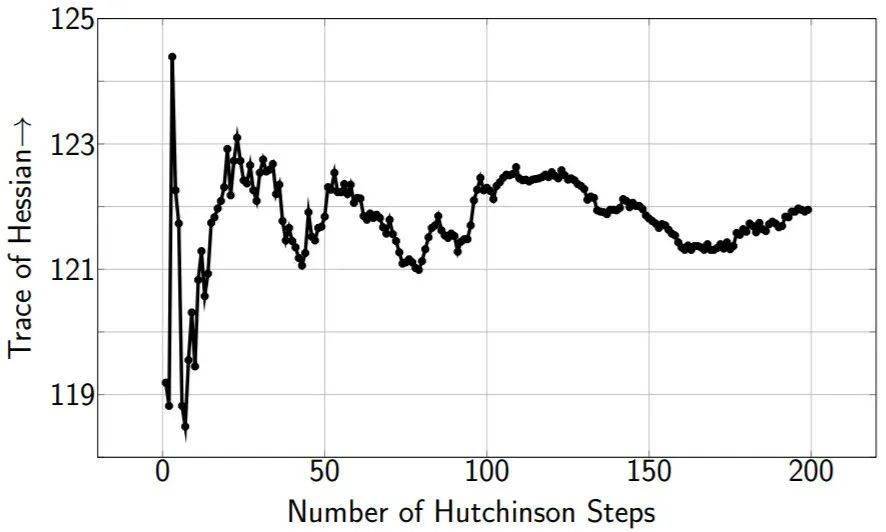
因为神经网络的权重很多 , 和Hessian矩阵相关的计算往往开销也很大 。 本文提出了使用Hutchinson方法来隐式的计算Hessian矩阵的迹 (即不显示地生成Hessian)。 如图所示 , Hutchinson方法可以在使用较少输入图片 , 以及较少迭代步数的情况下收敛 , 从而可以更加快速的计算Hessian矩阵的迹 。
文章图片
文章图片
知道了每一层对应的敏感程度之后 , 可以得到层与层之间的相对精度 , 但是每一层具体使用多少量化位宽仍需要人工确定 。 比如知道了第4层比第16层敏感需要给第4层更多的量化位宽 , 但依旧不能确定具体第4层是用6比特还是8比特 。 本文证明下面的基于Hessian矩阵的平均迹的评价标准 (metric) 可以很好地描述二阶扰动 , 从而可以将确定量化位宽的问题转化为一个整数规划问题 , 即找到满足压缩率限制条件的、使总二阶扰动最小的量化位宽的解 。
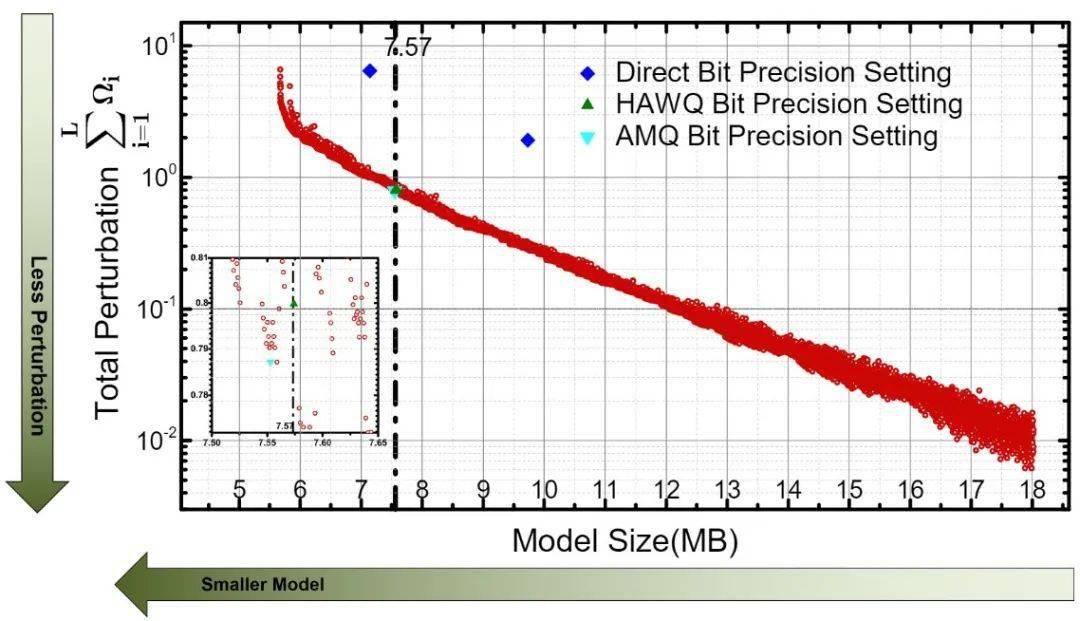
HAWQV2中描述了这个整数规划问题的一种高效解法 , 并将得到的结果表示成一个帕累托最优边界 (Pareto Frontier)。 如图所示 , 横轴是量化模型的最终尺寸 , 纵轴是总的二次扰动值 , 图中的每一个点都代表着一个量化位宽分配方案 。 可以看到 , 最小的量化模型对应着最大的总二阶扰动 , 而大的量化模型一般具有小的总二阶扰动 。 根据实际情况的需求 (比如要求模型大小要小于8MB) 可以选择满足条件且总二阶扰动最小的点作为最终的混合精度量化方案 。
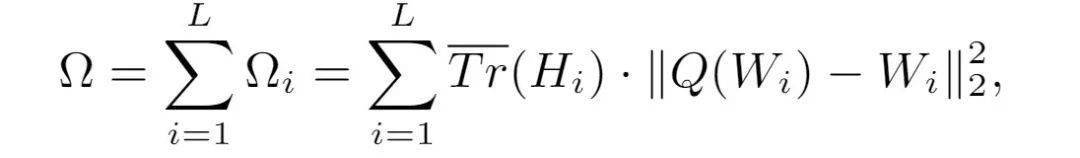
文章图片
文章图片
三、实验结果
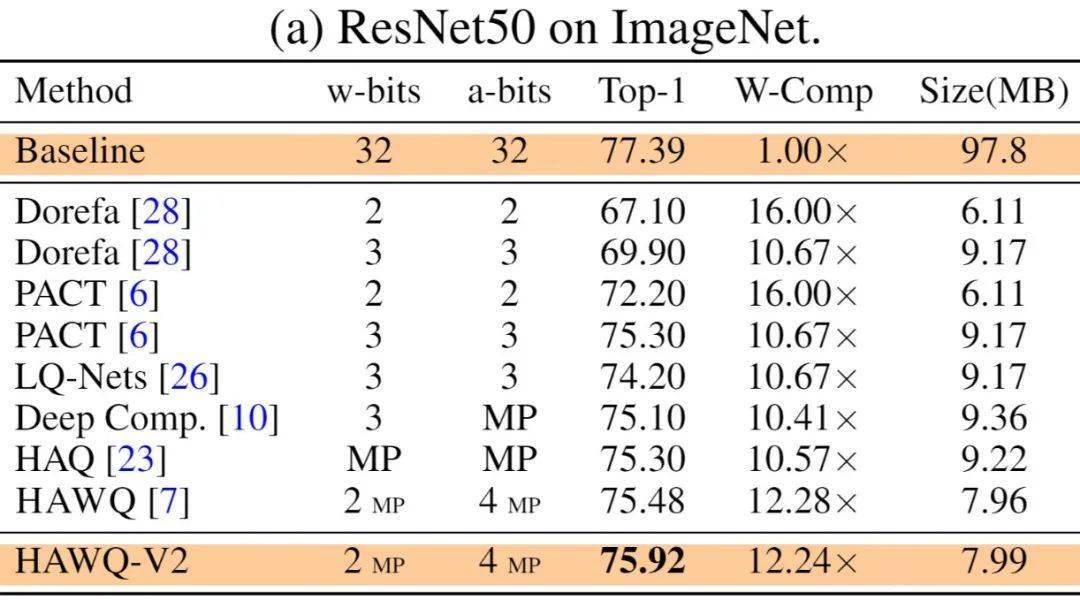
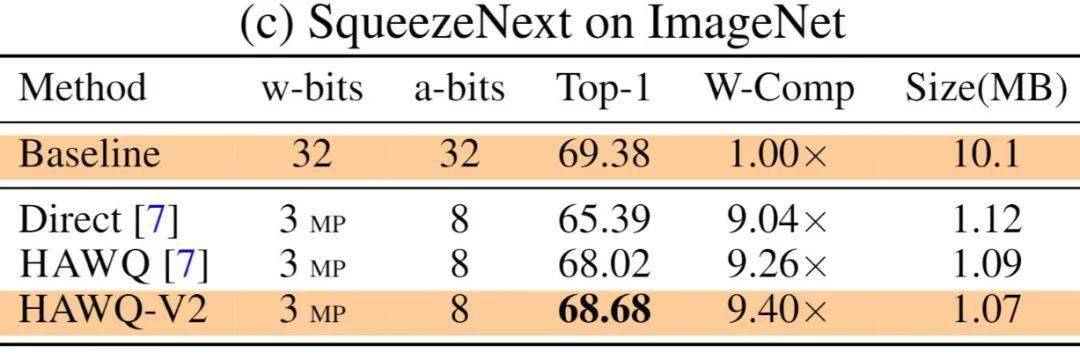
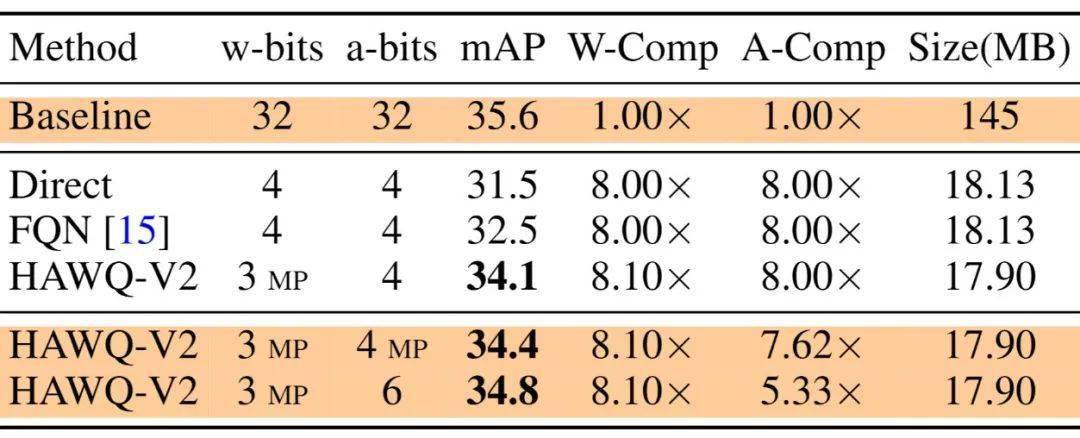
本文提出的方法HAWQV2使用经典的量化模拟训练 (Quantization-Aware Training), 采用标准训练超参数 , 只针对混合精度量化方案做出自动优化 。 HAWQV2在不同的神经网络模型 (ResNet50 , InceptionV3 , SqueezeNext , RetinaNet), 以及不同的任务 (物体分类ImageNet , 目标检测Microsoft COCO) 上面泛化能力很好 。 对于ResNet50 (预训练模型98MB), HAWQV2的8MB量化模型可以在ImageNet上实现75.2%的Top-1精确度 。 SqueezeNext是一个轻量级模型 (预训练模型10MB), HAWQV2的1MB量化模型可以在ImageNet上达到68.7%的Top-1精确度 。 在目标检测领域 , RetinaNet是一个很常用的模型 (预训练模型145MB), HAWQV2的18MB量化模型可以在MS COCO上实现34.1mAP 。 对于自然语言处理、Hessian敏感度分析依然适用 , 文献[2] (Q-BERT) 中使用类似的方法在各种下游任务 (语言标注 , 情感分类 , 问答等) 取得了很好的 (SOTA) 量化结果 (比如25MB的压缩版BERT)。
文章图片
文章图片
文章图片
四、结 语
本文提出了一种基于Hessian的敏感度分析方法来解决混合精度量化问题 。 具体而言 , 文章证明了Hessian矩阵的迹可以表征神经网络中一层的敏感程度 , 从而可以对敏感的层给予高量化位宽 , 而对不敏感的层给予低量化位宽 。 文章中提出了高效计算Hessian矩阵平均迹的方法 , 并基于此给出了可以自动确定混合精度的整数规划方案 。 文章中的方法HAWQV2在不同模型以及不同任务上取得了很好的 (SOTA) 量化效果 。
参考文献
[1] HAWQ: Hessian AWare Quantization of Neural Networks with Mixed-Precision, ICCV 2019.
[2] Q-BERT: Hessian Based Ultra Low Precision Quantization of BERT, AAAI 2020.
//
作者简介
【混合|伯克利人工智能实验室提出HAWQ: 基于Hessian矩阵的全自动混合精度量化方法】董镇 , 伯克利人工智能实验室 (BAIR) 三年级博士生 , 2018年本科毕业于北京大学EECS 。 目前的研究方向是高效神经网络(Efficient Deep Learning) , 模型压缩(Model Compression) , 软件硬件协同设计(HW-SW Co-Design & NAS) 。
推荐阅读
- 人工智能|聚焦车载人工智能计算芯片研究 推进汽车产业高质量发展
- 娱乐性|新华全媒+|探秘冬奥会“黑科技”:当冰壶遇上人工智能
- 市民|大数据、人工智能带来城市新变化 科技赋能深化文明成效
- 科研机构|人工智能点燃哈尔滨高质量发展新引擎
- 可持续性|人工智能将重塑健康管理,业内专家认为可持续性是最大挑战
- 策源|上海人工智能规上产业规模到2025年达到4000亿元
- 敏捷|上海人工智能“十四五”规划发布:集聚超20个国际顶尖团队
- 人工智能|佳都科技:已参与全国69个城市的智慧城市建设
- 数智|【受尊敬企业会客厅】 陈明键:在元宇宙,打造用人工智能发现药物的“乙世界”
- 人工智能|29岁当博导







