枢纽|普林斯顿研究“最小值”：平方和的破局，二次和三次优化问题的极限_

文章插图

多目标优化是各个领域中普遍存在的问题，每个目标不可能都同时达到最优，并且有现实应用的时效。各个因素必须各有权重。在困局中，平方和方法可用来寻找局部最优解。

编译 | 吴彤
编辑 | 维克多

生命是一连串的优化问题，下班后寻找回家的最快路线；去商店的路上权衡最佳性价比，甚至当睡前“玩手机”的安排，都可以看做优化问题。

优化问题的同义词是找到解决方案，有无数学者想探求在最短时间内，找到最好的解。但最新研究指出，一些二次优化问题，例如变量对可以相互作用的公式，只能“按部就班”找到局部最优解。换句话说“不存在快速计算方法”。
好消息是，另一项研究发现对于三次多项式下的优化问题，存在快速求解的方法。具体而言，可以通过使用平方和检验（sum-of-squares test）找到某些多项式的最低点，进而搜索三次函数的局部最优解。
两项研究时隔两天，出自于同一研究团队：普林斯顿大学的Amir Ali Ahmadi和他的前学生Jeffrey Zhang。

文章插图

Amir Ali Ahmadi和他的前学生Jeffrey Zhang

Amir Ali Ahmadi是普林斯顿大学运筹学与金融工程系教授，在加入普林斯顿大学之前，曾是IBM Watson研究中心的Goldstine研究员，其对优化理论，动力学和控制的计算以及算法和复杂度有很深的造诣。Jeffrey Zhang是卡内基梅隆大学的客座教授，研究领域包括博弈论、计算复杂性、多项式优化等等。

两篇“涉事”论文分别是：
论文1：On the complexity of finding a local minimizer of a quadratic function over a polytope
贡献：判定二次函数在(无界)多胞形（ polyhedron）上是否有局极小值，以及判定四次多项式是否有局部极小值属于NP难。
论文链接：https://arxiv.org/abs/2008.05558
论文2：Complexity aspects of local minima and related notions
贡献：证明了在三次多项式中，某些优化问题容易处理，且给出了寻找三次多项式局部极小值的一个充要条件。
论文链接：https://arxiv.org/abs/2008.06148
【枢纽|普林斯顿研究“最小值”：平方和的破局，二次和三次优化问题的极限】这两篇论文，一前一后，证明了复杂性计算研究的现状：某种类型的优化问题很容易解决，而某种类型的问题则必然很难解决。更进一步，他们为从金融到自动系统等各个领域的优化问题确定了新的边界。

生活中的优化问题

假设一家汽车厂只生产两种车型，便宜版和豪华版。豪华版的售价高于便宜车，但生产成本更高，生产时间也更长。那么两种车型应该各生产多少?
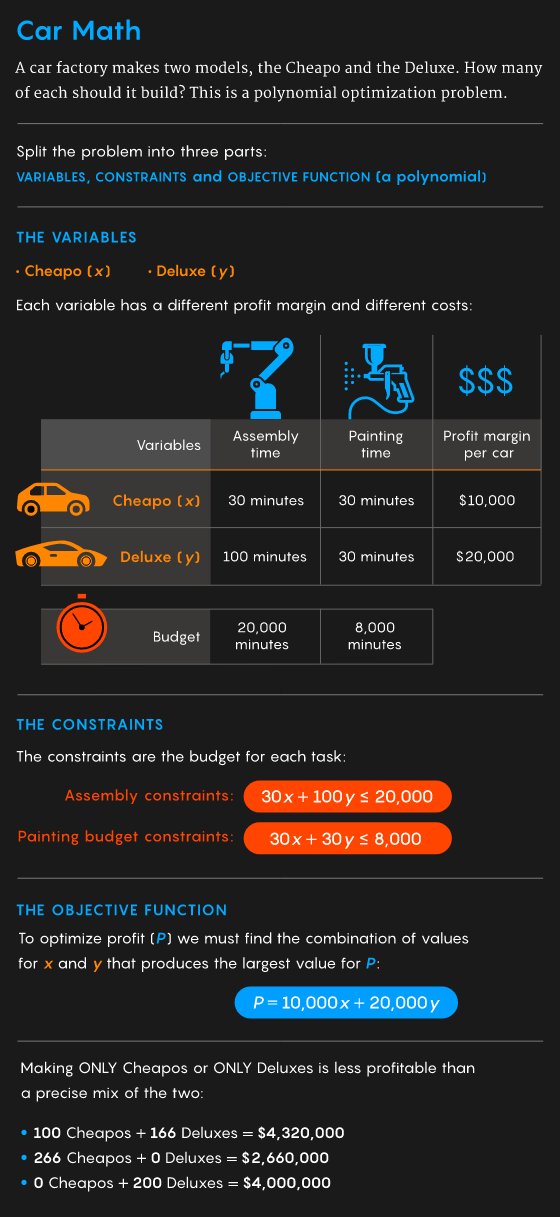
这个问题可以转化为一个用多项式表达的优化求解问题。
首先，这个问题可以分解为三个元素：