
文章图片
文章图片
我们宇宙的“可知性”有一个基本限制 , 海森堡不确定性原理告诉我们 , 当我们试图更精确地确定一个属性 , 它对应的属性就越难以确定 。 简而言之 , 完全知道一个粒子的位置意味着它的速度是不可知的 。 更进一步来说 , 未测量的属性不仅是不确定的 , 而且根本上是未定义的 , 这方面最深刻的例证之一是著名的双缝实验 。
一个粒子 , 比如一个光子或一个电子 , 穿过一个包含两个狭缝的屏障到后面的屏幕 。 它的初始位置和最终位置是已知的 , 但它之间的路径是什么?它穿过哪个狭缝?只有当它们中的每一个都穿过两个狭缝时 , 才能解释由屏幕上的粒子产生的干涉图案 。 不过此时我们不能把它当作粒子 , 而是作为填充中间空间的波 , 穿过一个狭缝的波的振幅与穿过另一狭缝的波的振幅相加来计算屏幕上粒子的位置 。
一个学生问:“如果在屏障上切第三条缝会发生什么?”显然 , 我们必须将穿过所有三个狭缝的波的振幅加在一起 。 那个学生继续问道:“但如果屏障上有四个、五个缝 , 甚至是无限的缝 , 连屏障都没有了 , 那应该怎么办呢?”没错 , 那个学生就是理查德·费曼 , 他刚刚概述了量子力学路径积分公式的基础知识 。 这是一个简单的想法 , 但它导致了有史以来最优雅的量子力学公式 , 并成为量子场论的关键 。
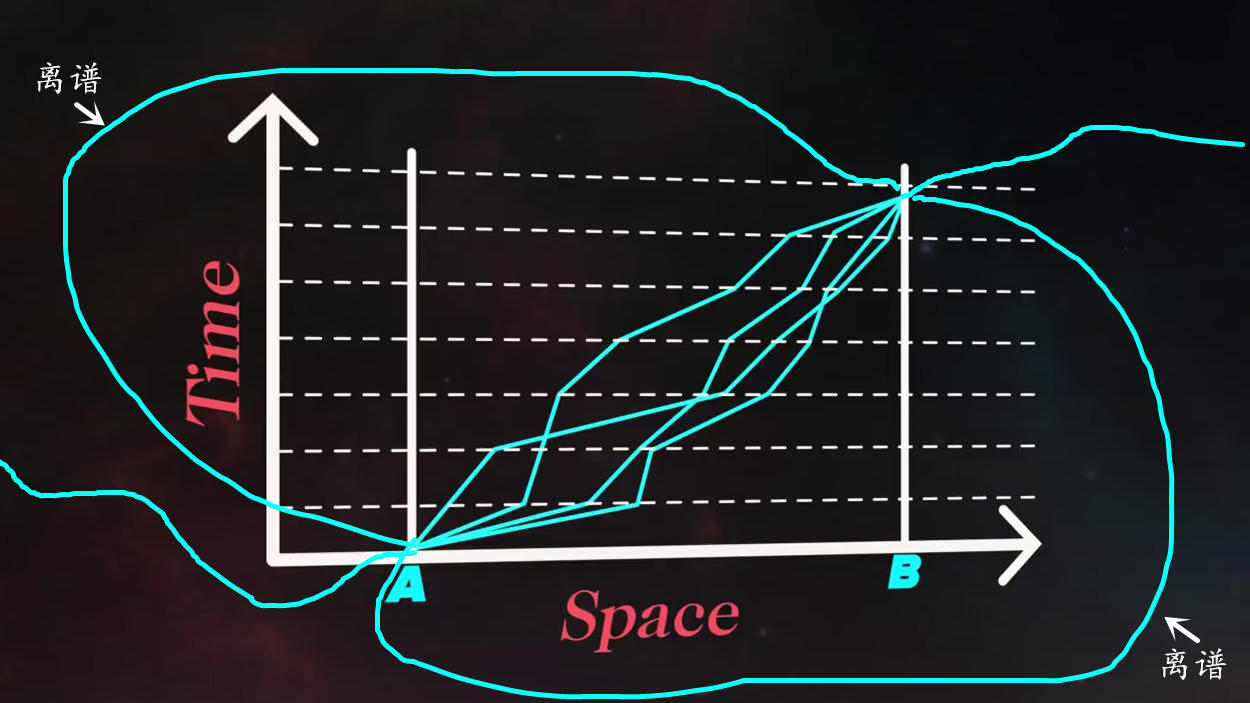
最小作用原理这个想法本质上是这样的:要知道粒子在两点之间传播的可能性 , 我们需要考虑所有可能发生的方式 。 双缝实验是一个特例 , 我们只考虑两种可能的路径 。 但是 , 当某物穿过空旷的空间时 , 它就像是穿过无数个有无限狭缝的屏障 , 有无限可能的路径 。 而费曼想出了一种方法来组合无限路径 , 以给出一个粒子到达其最终目的地的非常真实、有限的概率 。
他的诀窍是将传播所花费的时间切成小间隔 , 并在每个时间步长上让粒子在空间中采取任何可以想象的直线步长 。 这给出了一组从起始点到终点的路径 , 其中一些看起来很正常 , 但大多数都是荒谬的 。 例如 , 有些路径会绕圈或绕道到达宇宙的边缘 。
【如果双缝实验扩展到无限个缝会发生什么?浅谈费曼路径积分】
路径积分公式的惊人之处在于 , 费曼添加了一个且只有一个真实物理 , 那就是“最小作用原理” 。 它指出 , 一个对象将始终遵循作用量最小化的路径 。 这个作用量很难定义 , 它与路径上动能和势能之间的传递以及行程时间成正比 。 对于大尺度经典宇宙 , 最小化适当时间可以推导出几乎所有运动方程 。 然而 , 在量子宇宙中 , 没有单一的路径 , 费曼转而使用量子作用来为单个粒子可以采取的每条无限路径分配一个重要性——权重 。 然后 , 利用微积分的奇迹 , 他能够将所有这些无限可能路径的贡献加起来 , 以找到一个粒子从起点到终点进行简单旅行的概率 。
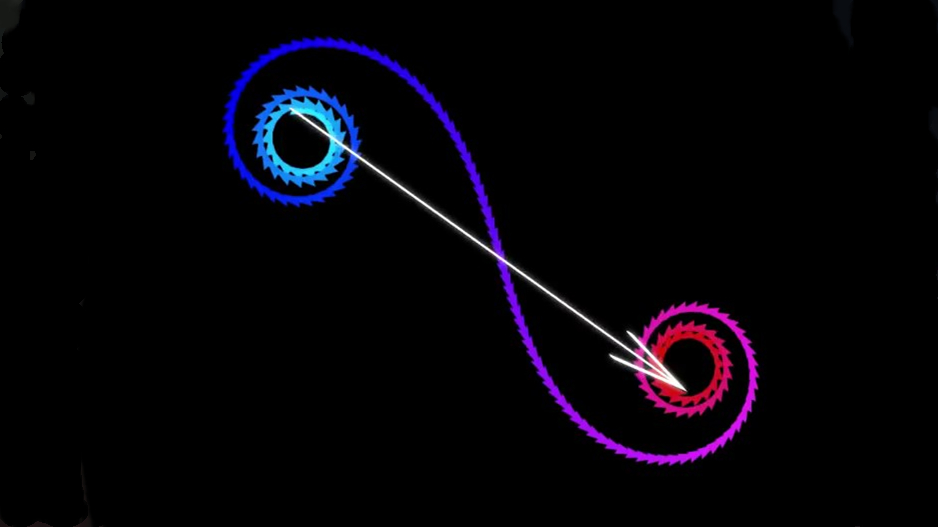
费曼的路径并不是每个都有单独的概率发生 。 相反 , 每条路径都为整个旅程贡献了我们所说的概率幅度 。 薛定谔的波函数和费曼的路径积分描述了这个概率幅度的东西 。 概率幅度是我们所说的复数 , 我们可以将每条路径的概率幅度想象成一个二维空间中某个长度和方向的箭头 。 每个箭头的总长度给出了该路径的概率 , 但是要获得粒子从起点到终点的总概率 , 需要将所有可能路径的概率幅度箭头首尾相连 。 连接该链的起点和终点的箭头长度表示所有路径的总概率 。
从无限到有限现在 , 当费曼用这个作用量计算出他无限路径的概率幅值时 , 神奇的事情发生了 。 所有疯狂的路径都相互抵消 , 只有最明智的路径——那些作用量最少的路径 , 才显着增加了概率 。 大尺度经典世界中熟悉的路径只是
费曼的路径积分公式使他能够从零开始推导出
推荐阅读
- 科学界震动,耶鲁大学发现量子力学不成立,宇宙宿命论找到证据
- 河北上空出现“怪象”,上千人拍到“南天门”,平行宇宙真存在?
- 量子力学:最小物质是夸克!它为什么是最小的粒子,不能再小了?
- 物理学停滞100年,三座大山难以逾越!根本原因是什么?
- 量子力学证实灵魂有不同形态?诺奖得主:人的大脑更像量子计算机
- 爱因斯坦口中的“鬼魅”被科学家首次拍到!或引发新的科技革命?
- 时间是静止的?一个颠覆人类认知的理论,可能引出全新的时间概念
- 男子心跳停7分钟后复活,醒后回忆“死亡世界”,死亡只是过程?
- 科学界于1927年召开了一次史诗级会议,留下一张珍贵照片







