文章图片
所有电气设备都需要能源 , 这是因为它们输出能量 。 灯泡产生光来照亮房间 , 微波炉产生微波辐射来加热饭菜 , 汽车产生动能来加速自身和乘客 。 基本上 , 每个电气设备都有一个能量输入 , 然后输出一部分有用的能量 , 而另一部分能量被耗散在摩擦、振动和热之类的东西上 。
但计算机处理器不同 , 它的功能不是点亮、加热某物或四处移动 。 当我们要求它计算123乘以456时 , 我们并不期望得到任何有用的能量 。 我们想要的只是让它操纵信息 , 翻转一组0和1并给我们答案 。 那么这是否意味着处理器使用的能量都是耗散的能量呢?如果我们有一个能消除这些能量损失的办法 , 那么计算机处理器可以完全不用能量运行吗?
【热力学:纯信息所消耗的能量】事实证明 , 答案是否定的 , 因为信息本身也有其自身的能源成本 , 这个成本是由一个称为兰道尔极限的原则设定的 。 该原则规定翻转一位信息所需的最小能量等于0.96×10^-23T焦耳 , 其中T是温度 。 在本文 , 我们将看到这个限制从何而来 。
逻辑门首先 , 我们必须要问 , 计算机在物理上是如何工作的?这就是逻辑门的用武之地 , 它是所有计算机的基本构建块 。 它的原理非常简单 , 接受两个输入 , 每个输入为1或0 , 然后生成一个相同形式的输出 , 也是1或0 。
逻辑门有多种不同的类型 , 用于不同的目的 , 每种都有不同的输入输出模式 。 我们可以将不同类型的逻辑门连接在一起 , 将输出连接到另一个门的输入 , 然后再连接到另一个 。 如此往复循环 , 我们就有一个逻辑网络 。 网络越大 , 它可以回答的问题就越复杂 。 将它构建得足够多 , 最终我们就可以问:什么是10 亿以下的最大素数 , 甚至什么是煮饭的最佳方法?
这就是现代计算机所拥有的东西:一个由数亿个逻辑门组成的网络 , 所有这些都协同工作以处理它给出的复杂信息 。
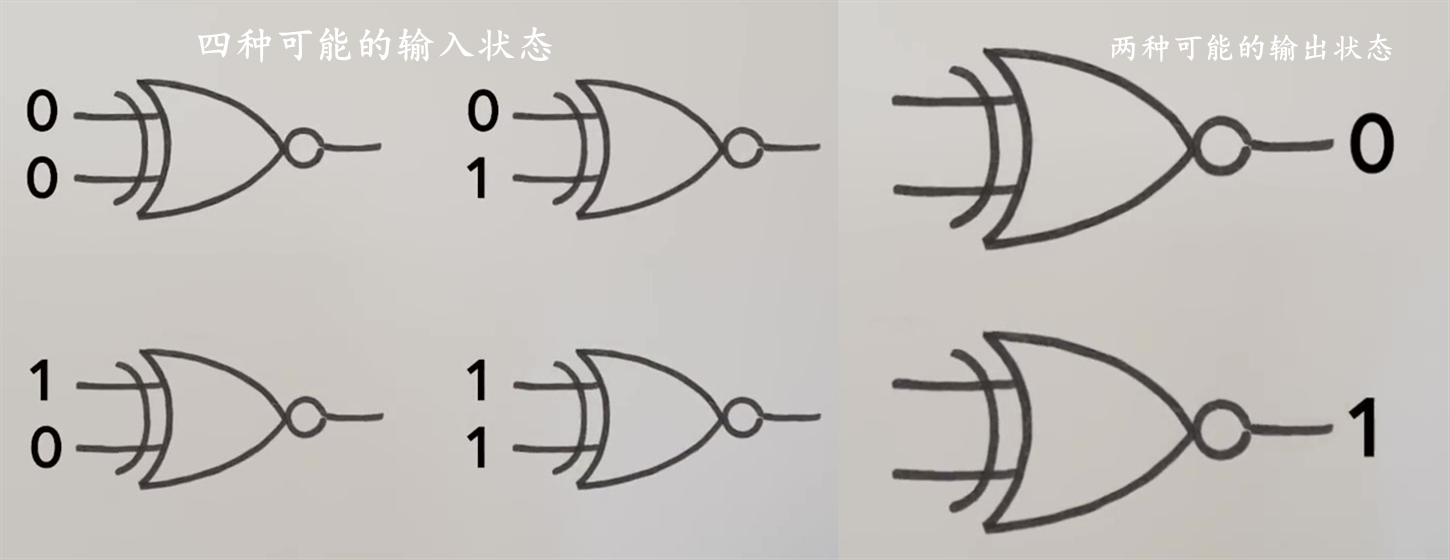
熵增原理那么这些逻辑门又与能量和信息有什么关系呢?回到单个的逻辑门 , 我们需要具体考虑它可以具有的输入和输出组合的数量 。 输入有两个位 , 每个位都可以独立地为1或0 , 我们总共得到四种可能性 。 输出更简单 , 由于门只输出一位 , 因此只有两种可能的输出状态:1或0 。
当我们开始谈论状态时 , 有个名叫玻尔兹曼的人就会变得非常感兴趣 。 玻尔兹曼是最早使用熵的概念的人之一 , 他提出了一个系统可以处于的状态越多 , 其熵就越高的想法 。 物理学中一个非常著名的定律是热力学第二定律 , 它指出系统的总熵只能增加或保持不变 , 它永远不会下降 。 在1870年代 , 玻尔兹曼写下了熵的方程:S=k_B(lnW) , 其中k_B是所谓的玻尔兹曼常数 , 而W是系统的状态数 。 让我们将其应用于我们上面说过的逻辑门 。
有四种可能的输入状态将其放入公式中 , 我们得到的熵为k_Bln4;执行操作后有两种可能的状态 , 这给出了k_Bln2的熵 。 在运算之后 , 门的熵实际上下降了 , 为了不违反热力学第二定律 , 它必须以某种方式产生熵的补偿增加 , 以便总熵不会减少 。
兰道尔极限具体来说 , 门产生单位热量等于熵的变化乘以系统的温度 , 这种热量的释放确保了整个系统的总熵不会变小 。 因此我们有兰道尔极限 , 我们需要消耗在逻辑门上运行一个操作的最小能量 。 1961年 , 物理学家兰道尔在IBM工作时首次提出了这个极限 。
值得注意的是 , 我们不必知道逻辑门的实际工作原理 , 它是否使用晶体管或光子并不重要 。 我们所知道的是 , 如果输出状态少于输入状态 , 则物理定律保证它必须消耗一定的能量 。 这就是为什么有时会说兰道尔极限给出了信息本身的能量值 。
推荐阅读
- 材料工程基础-重点
- 火星上喷出1500公里长的白烟,那是“火星人”在生火吗?
- 探索浩瀚宇宙的韦伯太空望远镜有多强?
- 霸总行为!他为斯坦福女友豪掷33亿盖研究所,招募150名科学家…
- 信息守恒与热力学第二定律,这些基本定律怎么可能是一致的呢?
- 庞加莱回归如果成立,人会在死后复活吗?答案:可以
- 对眼镜蛇来说,人类“太大”不符合食物标准,但别把它们惹急了
- 生命只能用生物学来理解吗?从物理学角度探讨生命的起源和本质
- 为何量子力学认为:-273.15℃,我们永远无法达到的低温极限?







