
文章图片

文章图片

文章图片
文章图片

文章图片

文章图片
在拓扑学当中有许多神奇的图形 , 其中最特别的 , 应该就是莫比乌斯环和克莱因瓶了 。 都是正反难分的代表 , 但偏偏前者我们可以很轻松地造出来 , 后者却如何努力都无法创造 。
这究竟是为什么呢?
莫比乌斯环和克莱因瓶
首先我们先来看看大家比较熟悉的莫比乌斯环 , 如今现在市面上其实有不少它的衍生产物 , 比如说“莫比乌斯环戒指” 。
莫比乌斯环 , 别称也叫莫比乌斯带 , 是由约翰·李斯丁和莫比乌斯在1858年发现的 。
当时他们利用普通的纸条进行实验 , 发现将纸条扭转180°之后 , 再将其两个接头处粘合在一起 , 就能够获得一个奇怪的“纸环” 。
为什么说这个纸环奇怪呢 , 是因为它只有一个单侧曲面 , 在这种情况下 , 如果将一只蚂蚁放在纸环上 , 并且让其在上面爬行 , 这只蚂蚁就可以不跨过任何的边缘 , 涉足纸环的所有地方 。
值得一提的是 , 在后续的研究当中 , 人们还发现 , 并不是只能将纸条旋转180° , 如果你乐意 , 转540°甚至900° , 得到的产物依旧是“莫比乌斯环” 。
因此对于莫比乌斯环 , 人们一直很感兴趣 , 认为它不止与数学有关 , 与物理学之类的也有密切的关系 。 在他们看来 , 这种处在三维欧几里得空间中的怪圈 , 实际上是一种二维单面环状结构 , 而我们或许可以依靠它来预测三维空间的某些结构 。
简单来说 , 如果哪天我们也走在一个像莫比乌斯环一样的公路上 , 那么可能永远都走不到尽头 。 因为它本身就是一个循环 , 在其中的我们会和蚂蚁一样 , 迷失方向 , 无法辨别起点和终点 。
其次再来看看克莱因瓶 , 相较于在不少地方都能见到的莫比乌斯环 , 克莱因瓶似乎有些冷门 。 不过 , 在拓扑学当中 , 它的地位还是很高的 , 甚至有某些人认为 , 克莱因瓶才是代表着“未来”的东西 。
克莱因瓶也叫克莱因壶 , 是德国几何学家菲利克斯·克莱因发现的 。 它的发现时间要比莫比乌斯环晚一些 , 大概是1882年 。 单从这个瓶子的外形来看 , 根本没什么稀奇 , 就只是形状比较诡异而已 。
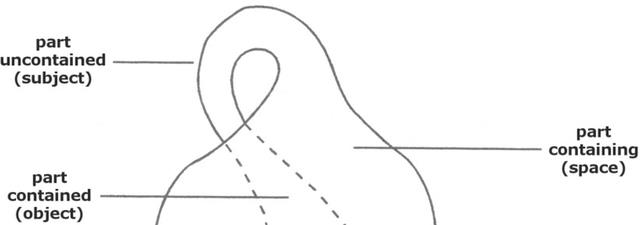
这是因为我们现在看到的克莱因瓶 , 根本算不上是它的真身 , 真正的克莱因瓶是不分“内外”的 。 并且 , 我们现在看到的那个插入瓶身当中的瓶颈 , 其实在拓扑图形中并没有这样“相交” 。
准确来说 , 这个瓶颈是通过第四个维度 , 来与瓶底实现相连的 。 这就意味着 , 进入其中的生物不需要飞越 , 便可以直接在内外表面反复横跳 。
对此大家可能感到无法理解 , 那我们就用常见的球状物体进行举例 。 如果我们把一只蚂蚁放在圆球的内部 , 就会发现它只能在内表面中爬行 。 想爬出来 , 除非利用口器将这个球咬出一个小洞 , 然后钻出来 。
可是克莱因瓶当中的蚂蚁就没有这种烦恼 , 在其表面不会终结的情况下 , 只要位于其中就能够随意涉足外表面和内表面 。 从某种角度上来说 , 这似乎也像莫比乌斯环上的虫子一样陷入了“无限循环” 。
其实从两位数学家对它们的发现历程 , 以及论证时所用的说法 , 就能看出前者是可以直接用实物扭出一个模型 , 后者虽能够造出来但是本质上却不是理论里的那个东西 。
那么 , 到底是什么原因导致了这种情况呢?
为什么克莱因瓶没办法被造出来?
从表面上来看 , 二者都是人们利用神奇的几何创造出来的东西 。 但是从实质上来说 , 二者涉及的维度确实有巨大差别的 ,







