薛定谔|薛定谔方程——量子力学皇冠上的明珠( 二 )
但后来 , 马克斯-博恩提出了一个想法:也许波函数与概率有关 。 但概率是实数 , 因此 , 他认为我们可以取其幅度的平方(每个复数和函数都有一个振幅)来获得一个实值 , 而不是直接将其值与概率联系起来 。 玻恩是正确的 。
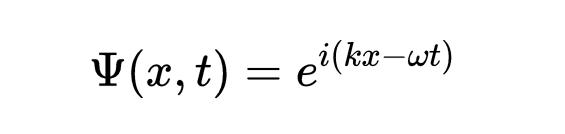
文章图片
一个具有动量p和能量E的粒子的波函数或德布罗意波
让我们回顾一下到目前为止我们所说的内容 。
亚原子粒子的行为与经典物体不同 。 它们既拥有类似波的特性 , 也拥有类似粒子的特性 。 此外 , 描述这种大小的粒子的方程在本质上是概率性的 。 薛定谔方程中的波函数是一个函数 , 其在空间和时间的某一点的值与粒子当时在那里的概率有关 。 它是如何相关的呢?它的大小的平方是概率密度(也就是每单位体积的概率) , 我们在空间的某个位置找到粒子的概率 。
所以这就是波函数所表达的 。 上过概率课程的人可以预见到它的一些特性 。 首先 , 我们对归一化的波函数感兴趣 。
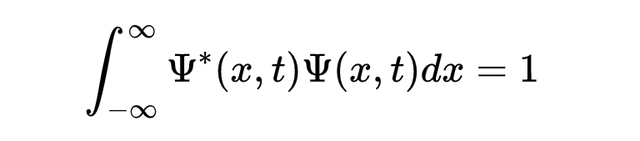
文章图片
波函数的归一化。 为了简单起见 , 这是一个一维(x维)的波函数
如果我们想一想 , 这是很直观的 。 由于波函数大小的平方(等于我们在积分里面看到的波函数与其共轭物的乘积)给出了概率密度 , 那么我们要求总的概率是1 。
我们已经“破译”了波函数背后的奥秘 。 现在让我们深入研究薛定谔方程 。
薛定谔方程
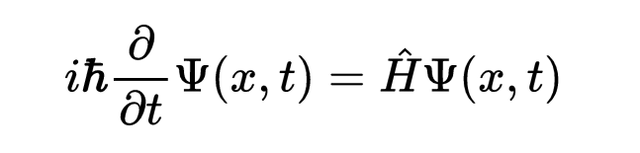
文章图片
记住我们到目前为止所说的一切 , 薛定谔方程描述了概率波的形式 , 它们是如何随时间演变的 , 以及它们在外部影响下的行为 。 让我们把它一点一点地分解 。
从左手边开始 , 我们首先遇到的两个符号是 "i"(虚数单位)和 "h"(普朗克常数) 。 尽管这些数字(符号)本身非常重要 , 但它们对于理解薛定谔方程并不重要 , 因此 , 我们在本文中不会涉及它们 。
我们遇到的下一个表达是波函数的时间导数 。 时间导数本质上是告诉我们某些东西相对于时间的变化速度 。 在这种情况下 , 是波函数的变化有多快 。
H上面加个“帽子”被称为哈密尔顿算子 。 对于那些不熟悉这个概念的人来说 , 简单地说 , 算子是一个函数 , 它的输入不是一个数字 , 而是另一个函数本身!它们将一个函数转换成另一个函数 。 例如 , 我们可以将运算符A定义为任意给定函数f = f(x)并将其乘以x的算子:
推荐阅读
- 水箱|七彩叮当除菌加湿器——水润加湿,让家庭生活更滋润
- 舍尔|编辑部荐书 | 编辑领读《哥德尔 艾舍尔 巴赫——集异璧之大成》
- 成果|数智电建,创享未来—博微智慧工地产品亮相首届中国电力建设数字经济发展论坛
- 服务|搜索引擎优化服务——如何检查表现不佳的内容,你知道多少?
- 信息|用数学视角谈一种最常见愚蠢表现——以偏概全
- 新浪科技综合|每天这样刷手机,人更容易抑郁——你可能已经这么做了
- 高中|学术大讲堂-第263期丨樊磊:高中信息技术新课程专题解读——人工智能(上)
- 市场|经济日报携手京东发布数据——智能电器引领健康生活
- 市政|数字市政典例——佛山首座数字化立体绿墙黑科技满满
- centre|英文论文写作工具——Seo Tools Centre三大功能介绍







