|一条线段和一条直线上的点一样多吗？_

【|一条线段和一条直线上的点一样多吗？】作者：大神团·冯伟
来源：新东方智慧学堂（ID：zhihuixuetang_xdf）
首先澄清一下标题的意思。
无论线段还是直线，我们都能从上取出无穷多个不重复的点。所以通常意义下的多或少在此是不适用的，我们实际在比较无穷的大小！那无穷怎么比大小呢？可能很多同学听说过所有整数和所有偶数的个数一样多这样的说法，这其实就是在比较无穷的大小。我们说他们个数相同，实际是在整数和偶数中建立了一一对应的关系。这很好理解，我们不用去数教室里有多张桌子，多少张椅子，只要知道每张桌子都配有一张椅子，即桌子椅子一一对应，就知道二者数量一样多。
所以一一对应是关键，而整数和偶数的这种一一对应关系几乎是显然的：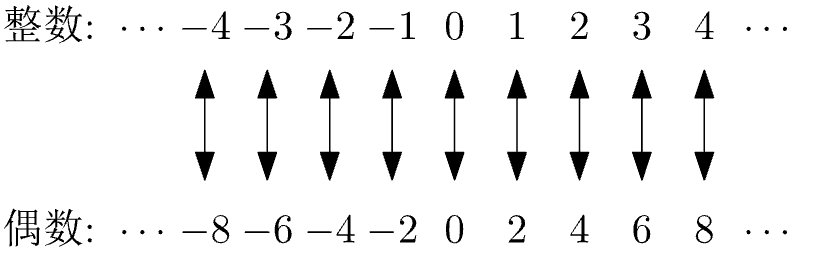

本文图片

下面我们就来寻找线段和直线间的一一对应关系，不过需要分几个步骤：

任意两条线段
可建立点之间的一一对应
我们可以将线段 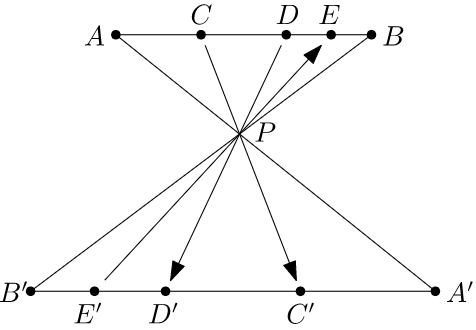$AB$ 和 $A'B'$ 反向平行放置， $AA'$ , $BB'$ 交于 $P$ 。于是从 $AB$ 上任取一点 $C$ ，连接 $CP$ 并延长可与 $A ' B'$ 有一交点 $C'$ 作为 $C$ 的对应点。显然 $AB$ 上不同的点 $C、D$ 在 $A' B'$ 上的对应点 $C'D'$ 也是不同的（单射) ，而 $A'B'$ 上任意一点 $E'$ 在 $AB$ 上也都有对应点 $E$ （满射），故我们建立了任意两条线段上的点之间的一一对应（双射）关系。

本文图片

开区间 $(?1,1)$
和直线可建立点之间的一一对应
回忆一下我们学过的正切函数，通过函数 $y=\tan\frac\pi x2$ ，我们可以在开区间 $(?1,1)$ 和 $y$ 轴上的点之间建立一种对应关系。
容易证明这种对应是一一对应：任取 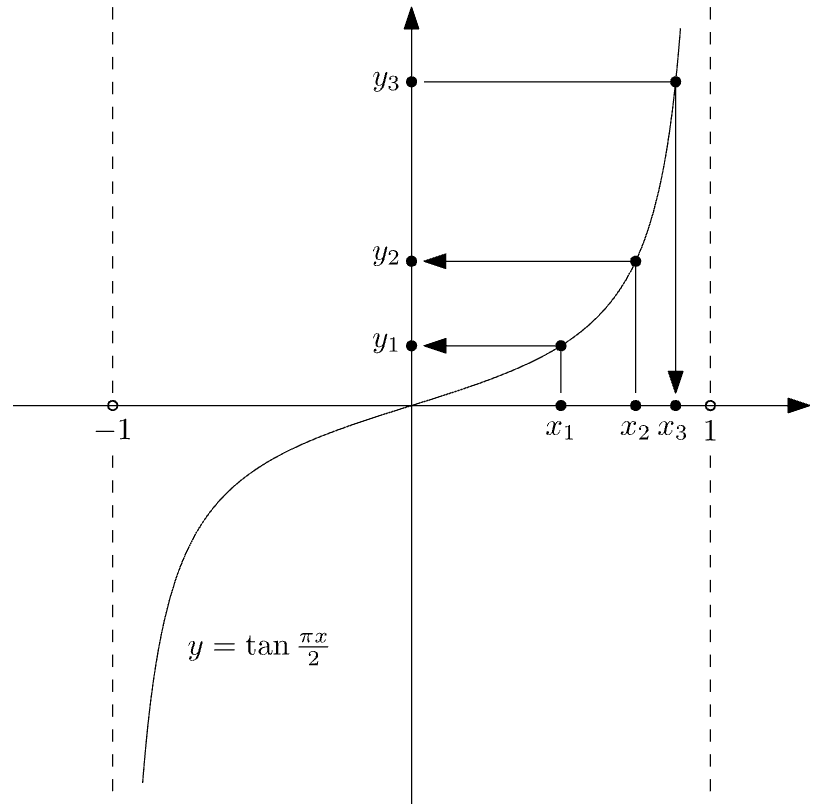$x_1, x_2,$ 且 $x_1≠x_2,$ 则由函数的严格单调知 $y_1=\tan\frac\pi x_12≠\tan\frac\pi x_22=y_2$ (单射) 。 $y$ 轴上任取一点 $y_3$ ，则存在唯一一点 $x_3$ 使得 $y_3=\tan\frac\pi x_32$ （满射）。故该对应为一一对应（双射）。

本文图片

线段 $[-1,1]$
和直线可建立点之间的一一对应
我们的目标看起来近在眼前了。

本文图片

因为根据第一步，任意长度线段都可以和线段 $[-1,1]$ 建立点之间的一一对应。而除去两个端点 $-1$ 和 $1$ 外的开区间 $(?1,1)$ 又能和直线（ y轴）建立一一对应，我们只需想办法把两个端点加进去。
在已经配齐桌椅的教室里加两把椅子，显然无论怎么匹配，桌子和椅子间都不能建立一一对应。因为总会有两把椅子无法和桌子配对。
但当我们面对的对象是无穷时，一些违反直觉的事情就会发生了。

|一条线段和一条直线上的点一样多吗？
本文图片

先来了解一下著名的希尔伯特无穷旅馆问题。
设想有一家旅馆，内设无限个房间，所有的房间也都客满了。这时有一位新客想订个房间。
这怎么实现呢？
只见旅馆主人把1号房间的旅客移到2号房间， 2号房间的旅客移到3号房间， 3号房间的旅客移到4号房间等等，这样一直移下去。
这样一来，新客就被安排住进了已被腾空的1号房间。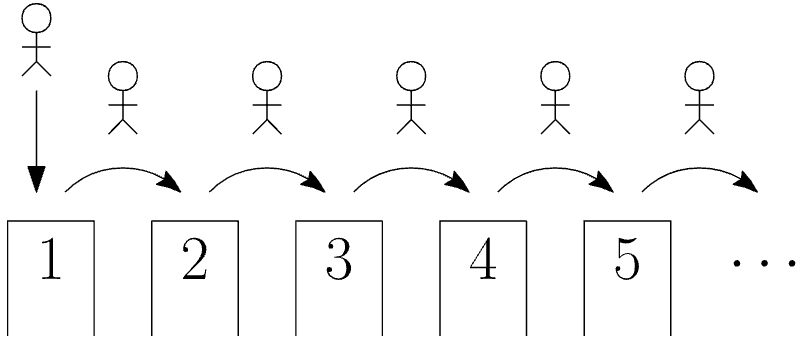

|一条线段和一条直线上的点一样多吗？
本文图片

现在，聪明的同学们想到如何把两个端点加入对应关系中去了吗？
只需构造一个希尔伯特旅馆就可以了！
我们把点 $\\frac12,\frac13,\frac14,\cdots$ 看作客人, 把 $y$ 轴上的对应点 $\\tan\frac\pi2*2,\tan\frac\pi2*3,\tan\frac\pi2*4\cdots$ 看作旅馆，现在要让新客 $\1$ 住进旅馆，只需修改对应关系，使 $1\rightarrow\tan\frac\pi2*2,\frac12\rightarrow\tan\frac\pi2*3,\frac13\rightarrow\tan\frac\pi2*4,\cdots$ 即可。
这些点以外的其他对应关系依然保持不变。
同理，我们也可以把 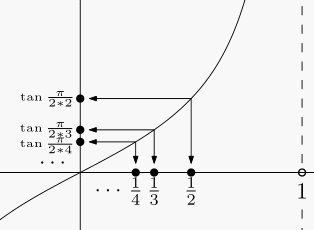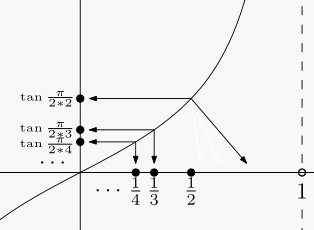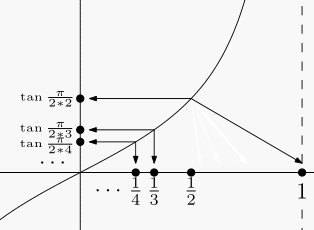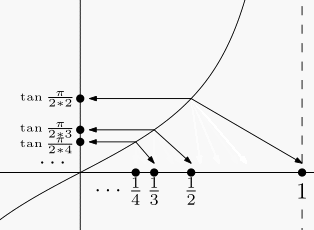$\-1$ 放进去。

|一条线段和一条直线上的点一样多吗？
本文图片

以上综合起来，我们就能把任意线段和直线建立点之间的一一对应了。
标题的问题也就这样解决了。
作者介绍：冯伟，新东方超尖生计划授课老师，清华硕士。全国初中数学、物理、化学三项竞赛一等奖，中国西部数学奥林匹克银牌，北京市大学生数学竞赛一等奖，全国大学生物理竞赛一等奖，清华大学优秀硕士毕业生。
来源：新东方智慧课堂
原文标题：一条线段和一条直线上的点一样多？90%的学霸都不会证明
编辑：hxg