|进展 | 二维非厄米系统奇异点及费米点的Nielson-Nanomiya定理_

和人一样，自然的规律也喜欢“成双成对” 。在格点规范场论中， Nielson-Nanomiya定理（或称Fermion doubling theorem, 费米子重叠定理）就是保证不同手性的费米子总是成双成对出现的一个重要概念，具体一点来说，就是在一个局域的，厄米的，以及平移不变的格点规范场论中，不同手性的费米子总是成对出现的。
过去的十多年， Nielson-Nanomiya定理在拓扑能带理论的发展过程中发挥了非常重要的作用，它保证布里渊区中拓扑荷总是成对出现的。比如对于一般的拓扑半金属，能带简并点总是成对出现；与此对应，每个能带简并点都可以定义一个拓扑荷，例如在外尔拓扑半金属中，拓扑荷可以定义成围绕外尔点的陈数（Chern number）。如图1所示， Nielson-Nanomiya定理保证了这些拓扑荷在整个布里渊区中求和一定等于零。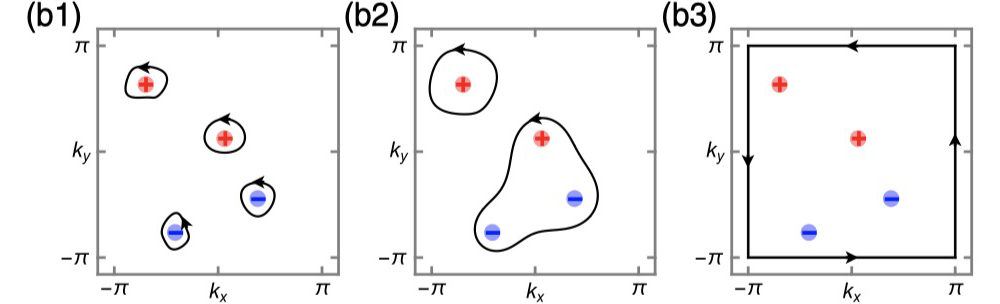

本文图片

图1: Nielson-Nanomiya定理中拓扑荷在布理渊区的分布示意图以及求和，红色和蓝色代表拓扑荷相反。有趣的是，对拓扑材料来说， Nielson-Nanomiya定理可以在材料的表面被破坏，这个破坏恰好反应了材料的拓扑结构。比如在时间反演不变的拓扑绝缘体的一个表面上，狄拉克点可以单独出现，出现这样的表面态和体态的能带拓扑是一一对应的，这就是拓扑能带理论中著名的体边对应。
Nielson-Nanomiya定理在非厄米拓扑系统中还成立吗？近年来，得益于人造材料和光子晶体的实验发展，非厄米系统受到了越来越多的关注，这个问题也很自然地成为非厄米系统的一个基本物理问题。非厄米系统中有一类被称为奇异点的特殊简并点，过去的研究已经表明在非厄米系统中依然可以定义奇异点的拓扑荷。但值得注意的是，过去针对非厄米系统拓扑荷的推广公式，并不能推导出有关奇异点的Nielson-Nanomiya定理。
最近，中国科学院物理研究所/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T06研究组胡江平研究员指导的博士生杨哲森（现卡弗里理论科学研究所博士后），与德国马普所的Schnyder研究员以及卡弗里理论科学研究所的邱靖凯研究员合作，借助于数学中关于多项式判别式的概念，得到多能带非厄米系统奇异点的普遍定义，并且证明了奇异点满足Nielson-Nanomiya定理，即，奇异点总是成对出现的，并且进一步指出过去研究的拓扑荷并非奇异点的性质，而是有关费米点的性质，澄清了费米点和奇异点之间的差别（图2）。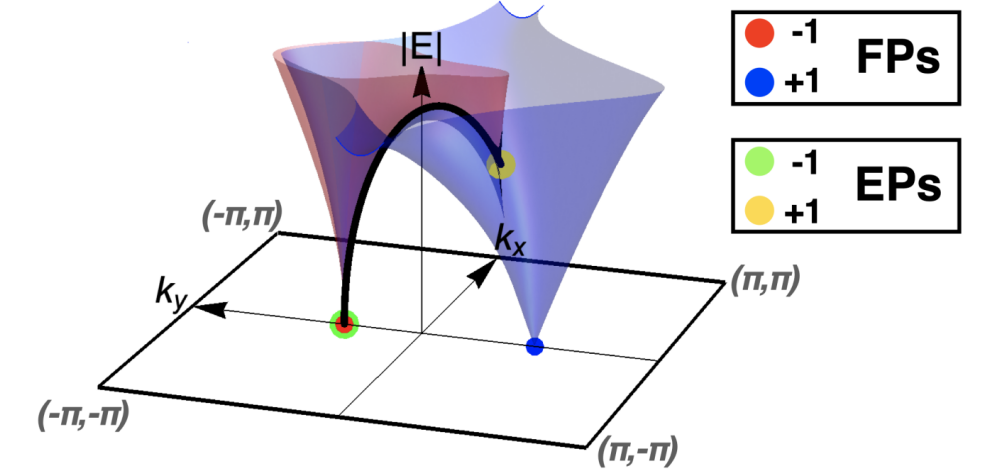

本文图片

图2: 两能带系统中费米点与奇异点的差别示意图；红、蓝曲面代表两个不同的能带；黄、绿两点代表成对的奇异点，中间黑线代表费米弧；而红、蓝两点代表成对的费米点。【|进展 | 二维非厄米系统奇异点及费米点的Nielson-Nanomiya定理】文章还进一步探讨了Nielson-Nanomiya定理在三维材料表面被破坏的情况，并澄清了诸多关于奇异点的特殊性质，为研究非厄米系统中有关奇异点的物理奠定了理论基础。相关研究成果发表于Phys. Rev. Lett. 126, 086401 (2021) ，并被选成期刊编辑推荐的文章。
该工作受到科技部重点研发计划（2016YFA0302400, 2017YFA0303100）、国家自然科学基金委员会（11674370, 11888101）和中国科学院（XXH13506-202, XDB33000000, XDB28000000）的资助。
论文链接：
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.126.086401
延伸阅读：http://www.iop.cas.cn/xwzx/kydt/202012/t20201201_5804194.htmlhttp://www.iop.cas.cn/xwzx/kydt/202011/t20201117_5750186.htmlhttp://www.iop.cas.cn/xwzx/kydt/202005/t20200511_5577472.html
编辑：hxg