平面|这些立体几何的方法技巧，收好，实用提分策略_表面积|立体几何|棱锥|技巧|性

文章图片

空间几何体的表面积和体积相关的问题一直是高中数学的重要内容，如何求棱柱、棱锥、棱台的表面积和体积，一般多采用面积累加的方式求解,特别地,若为正棱柱（锥、台）,各侧面积相等,可用乘法计算;计算其体积时,关键是求底面积和高。
如何正确求出几何体的侧面积和全面积，关键要对知识有本质上的认识，如几何体侧面积是指(各个)侧面面积之和，而全面积是侧面积与所有底面积之和．对侧面积公式的记忆，最好结合几何体的侧面展开图来进行。
应掌握平面基本性质、空间两条直线、直线和平面、两个平面的位置关系（特别是平行和垂直关系）以及它们所成的角与距离的概念。同时，要能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定，进行论证和解决有关问题。

文章图片

立体几何有关的高考试题分析，典型例题1：
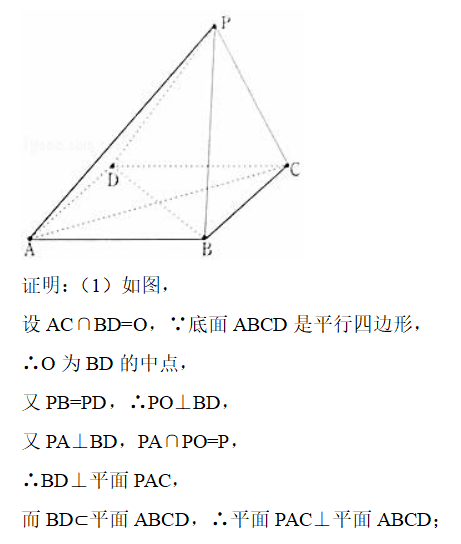
已知在四棱锥P﹣ABCD中，底面ABCD是平行四边形，且有PB=PD ， PA⊥BD．
（1）求证：平面PAC⊥平面ABCD；
（2）若∠DAB=∠PDB=60° ， AD=2 ， PA=3 ，求四棱锥P﹣ABCD的体积．

文章图片

文章图片

考点分析：
棱柱、棱锥、棱台的体积；平面与平面垂直的判定．
题干分析：
（1）设AC∩BD=O ，则O为BD的中点，由PB=PD ，得PO⊥BD ，再由已知PA⊥BD ，利用线面垂直的判定可得BD⊥平面PAC ，进一步得到平面PAC⊥平面ABCD；
（2）由（1）知，平面PAC⊥平面ABCD ，可得BD⊥AC ，则AB=AD ，得到四边形ABCD为菱形，然后求解三角形可得△POA的面积，再由等积法求得四棱锥P﹣ABCD的体积．

文章图片

立体几何有关的高考试题分析，典型例题2：
如图，已知三棱锥P﹣ABC ， BC⊥AC ， BC=AC=2 ， PA=PB ，平面PAB⊥平面ABC ， D、E、F分别是AB、PB、PC的中点．
（Ⅰ）证明：PD⊥平面ABC；
（Ⅱ）若M为BC中点，且PM⊥平面EFD ，求三棱锥P﹣ABC的体积．

文章图片

考点分析：
棱柱、棱锥、棱台的体积；直线与平面垂直的判定．
题干分析：
（Ⅰ）由PA=PB ， D为AB中点，可得PD⊥AB ，再由面面垂直的性质可得PD⊥平面ABC；
（Ⅱ）设PM交EF于N ，连接DM ， DN ，由线面垂直的性质得到PM⊥DN ，由已知可得DN垂直平分PM ，故PD=DM ，求出DM ，进一步求得PD．即三棱锥P﹣ABC的高，然后由三棱锥体积公式求得三棱锥P﹣ABC的体积．

文章图片

立体几何有关的高考试题分析，典型例题3：
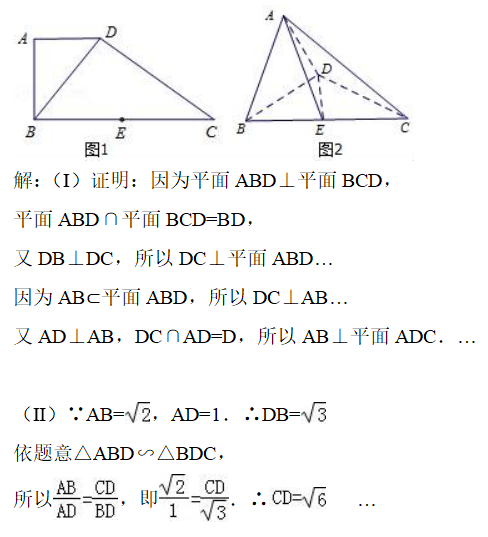
如图1 ，在直角梯形ABCD中， AD∥BC ， AB⊥BC ， BD⊥DC ，点E是BC边的中点，将△ABD沿BD折起，使平面ABD⊥平面BCD ，连接AE ， AC ， DE ，得到如图2所示的几何体．
（Ⅰ）求证：AB⊥平面ADC；
（Ⅱ）若AD=1 ， AB=√2 ，求二面角B﹣AD﹣E的大小．

文章图片

文章图片

考点分析：
二面角的平面角及求法；直线与平面垂直的判定．
题干分析：
（Ⅰ）只需证明DC⊥AB ，由AD⊥AB ， DC∩AD=D ，得AB⊥平面ADC
【平面|这些立体几何的方法技巧，收好，实用提分策略】（Ⅱ）易得∴CD=√6 ，建立空间直角坐标D﹣xyz ，则D（0 ， 0 ， 0）， B（√3 ， 0 ， 0）， C（0 ， √6 ， 0）， E（√3/2 ， √6/2 ， 0）， A（√3/3,0.√6/3），求出平面DAB的法向量，平面ADE的法向量，求得二面角B﹣AD﹣E的大小为60° 。

平面|这些立体几何的方法技巧，收好，实用提分策略

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)