热点|学霸必会的考点，也是高考热点，现在看还来得及_不等式|问题|函数|考点|导数

文章图片

导数是研究函数性质的重要而有力的工具，特别是对于函数的单调性，以“导数”为工具，能对其进行全面的分析，为我们解决求函数的极值、最值提供了一种简明易行的方法，进而与不等式的证明，讨论方程解的情况等问题结合起来，极大地丰富了中学数学思想方法.复习时，应高度重视以下问题：
1、求函数的解析式；
2、求函数的值域；
3、解决单调性问题；
4、求函数的极值（最值）；
5、构造函数证明不等式。
导数考查范围：
1、了解导数概念的某些实际背景（如瞬时速度、加速度、光滑曲线切线的斜率等）；掌握函数在一点处的导数的定义和导数的几何意义；理解导函数的概念。
2、熟记基本导数公式；掌握两个函数和、差、积、商的求导法则。了解复合函数的求导法则，会求某些简单函数的导数。
3、理解可导函数的单调性与其导数的关系；了解可导函数在某点取得极值的必要条件和充分条件（导数在极值点两侧异号）；会求一些实际问题（一般指单峰函数）的最大值和最小值。

文章图片

导数有关的高考试题分析，典型例题1：
已知函数f（x）=m/x+xlnx（m＞0）， g（x）=lnx﹣2．
（1）当m=1时，求函数f（x）的单调区间；
【热点|学霸必会的考点，也是高考热点，现在看还来得及】（2）设函数h（x）=f（x）﹣xg（x）﹣√2 ， x＞0．若函数y=h（h（x））的最小值是3√2/2 ，求m的值；
（3）若函数f（x）， g（x）的定义域都是[1 ， e] ，对于函数f（x）的图象上的任意一点A ，在函数g（x）的图象上都存在一点B ，使得OA⊥OB ，其中e是自然对数的底数， O为坐标原点，求m的取值范围．

文章图片

文章图片

考点分析：
利用导数求闭区间上函数的最值；利用导数研究函数的单调性．
题干分析：
（1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可；
（2）求出h（x）的导数，解关于导函数的不等式，求出函数的单调区间，求出h（x）的最小值，从而求出m的值即可；
（3）根据OA和OB的关系，问题转化为x2/2﹣x2lnx≤m≤x2（e﹣lnx）在[1 ， e]上恒成立，设p（x）=x2/2﹣x2lnx ，根据函数的单调性求出m≥p（1）=1/2 ，设q（x）=x2（e﹣lnx），根据函数的单调性求出m≤q（1），从而求出m的范围即可．

文章图片

导数有关的高考试题分析，典型例题2：
已知函数f（x）=ax2+cosx（a∈R）记f（x）的导函数为g（x）
（1）证明：当a=1/2时， g（x）在R上的单调函数；
（2）若f（x）在x=0处取得极小值，求a的取值范围；
（3）设函数h（x）的定义域为D ，区间（m ， +∞）?D．若h（x）在（m ， +∞）上是单调函数，则称h（x）在D上广义单调．试证明函数y=f（x）﹣xlnx在0 ， +∞）上广义单调．

文章图片

文章图片

考点分析：
利用导数研究函数的极值；利用导数研究函数的单调性．
题干分析：
（1）求出函数的导数，根据导函数的符号，求出函数的单调区间即可；
（2）求出函数的导数，通过讨论a的范围求出函数的单调区间，单调函数的极小值，从而确定a的具体范围即可；
（3）记h（x）=ax2+cosx﹣xlnx（x＞0），求出函数的导数，通过讨论a的范围结合函数的单调性证明即可．

文章图片

导数有关的高考试题分析，典型例题3：
已知函数f（x）=xex﹣a（lnx+x）．
（1）若函数f（x）恒有两个零点，求a的取值范围；
（2）若对任意x＞0 ，恒有不等式f（x）≥1成立．
①求实数a的值；
②证明：x2ex＞（x+2）lnx+2sinx．

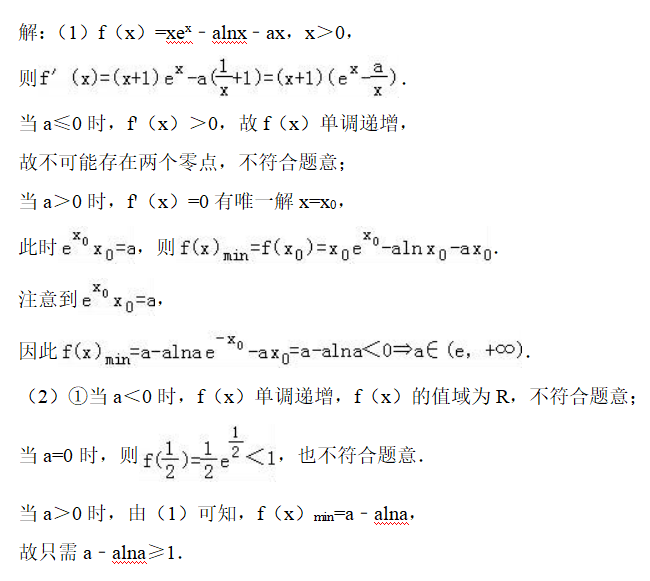
文章图片

文章图片

考点分析：
导数在最大值、最小值问题中的应用；函数恒成立问题；不等式的证明．
题干分析：
（1）利用导数的运算法则可得f′（x），对a分类讨论，当a≤0时， f'（x）＞0 ，故f（x）单调递增，舍去．当a＞0时， f'（x）=0有唯一解x=x0 ，此时求出极值，进而得出答案．
（2）①当a≤0时，不符合题意．当a＞0时，由（1）可知， f（x）min=a﹣alna ，故只需a﹣alna≥1．令t=1/a ，上式即转化为lnt≥t﹣1 ，利用导数研究其单调性极值即可得出．
②由①可知x2ex﹣xlnx≥x2+x ，因而只需证明：?x＞0 ，恒有x2+x＞2lnx+2sinx．注意到前面已经证明：x﹣1≥lnx ，因此只需证明：x2﹣x+2＞2sinx．对x分类讨论，利用导数研究函数的单调性极值即可得出。

热点|学霸必会的考点，也是高考热点，现在看还来得及

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)