哥德巴赫猜想|同样是关于质数，为啥哥德巴赫猜想比我有名？( 二 )_数学

这是一个很准确的近似。然而，要精确地理解质数定理告诉我们的东西，我们需要说出我们所说的“一个准确的近似”是什么意思。质数定理并不是说，对于一个给定的整数n ，真值和我们的近似值之间的差值接近 0。相反，它告诉我们关于“近似值占真值的百分比是多少?”的问题。回到我们 n=1000 的例子，真值是 168 ，近似值是 145。因此，近似构成的比例：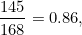

近似值占真实值的 86%，不错。当 n=100000 时，包含 100000 的质数是 9592，这是真值，估值是 8686。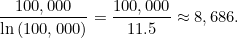

在这种情况下，估值占真值的 90%。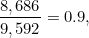

这相比于 n=1000 的情况，比例从 86% 提升到了 90%。一般来说，质数定理告诉我们，对于 n 很大的情况，n/ln(n) 得到的近似值几乎是真值的 100%。事实上，你可以让它接近 100% ——只要你选择足够大的 n。
【哥德巴赫猜想|同样是关于质数，为啥哥德巴赫猜想比我有名？】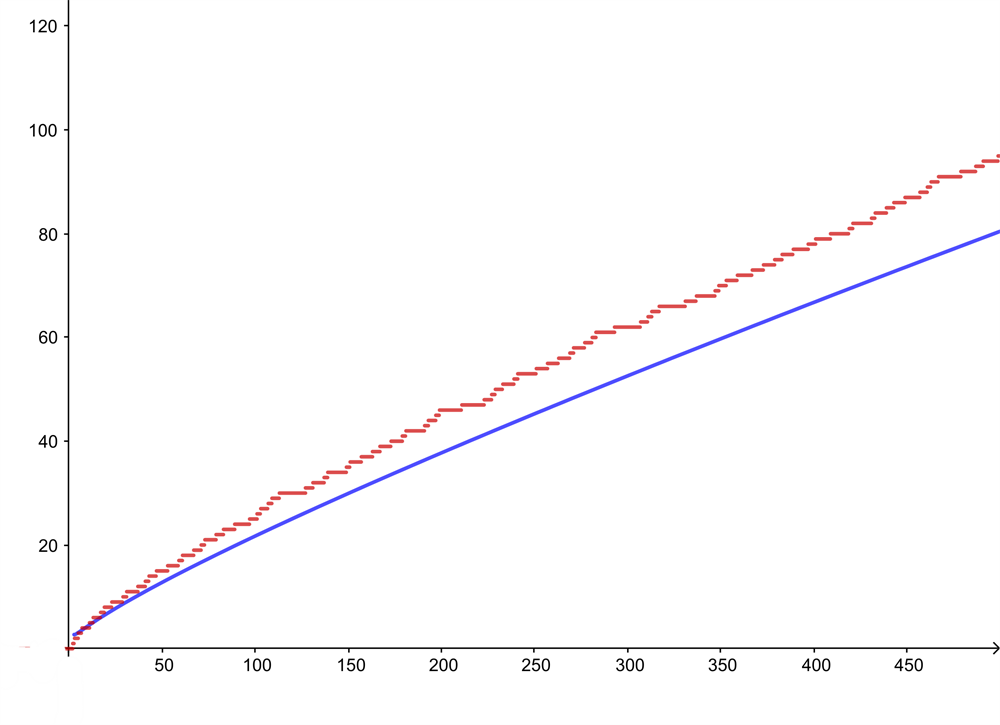

红色曲线显示的是小于或等于n的质数数目，其中横轴表示 n。蓝色曲线给出 n/ln(n) 的值。真实结果和近似结果之间的差值随着 n 的增长而增加，但两者之间的比值趋于 1。为了用数学符号来描述素数定理在数学上的辉煌，让我们先用表示小于或等于的质数的数目。这个定理可以用公式表述：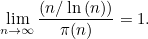

(1)如果你懂一点微积分你就会知道你可以交换分子和分母，此时表达式 (1) 等于：

(2)素数定理通常用第二个表达式 (2) 来表述，有时也写成：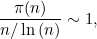

表示：“当 n 趋近于无穷大时，n/log(n) 趋近于 π(n) ” 。作者：Marianne翻译：C&C审校：zhenni原文链接：https://plus.maths.org/content/maths-minute-prime-number-theoremhttps://plus.maths.org/content/maths-minute-how-many-primes
编辑：zhenni
想了解更多精彩内容，快来关注中科院物理所

哥德巴赫猜想|同样是关于质数，为啥哥德巴赫猜想比我有名？( 二 )

推荐阅读

如何找寻自我

缝纫机调线器怎么安装平车方法如何

强组词强字组词

火笋鸡翅的做法（增肥食谱）

闺女生日快乐祝福语朋友圈

LV请来潮牌设计师做艺术总监，看中的是啥

老虎豆怎么做好吃老虎豆图片怎样弄来吃

暖气有流水声是什么原因

皮球是什么体

手机怎样开通QQ空间

男生发mua说明 mua是什么意思

手指盖凹陷怎么回事

对自己的生活失去掌控咋调整

小米10s怎么没有月亮模式

我想找个偏僻的地方搞养殖！有没有推荐的地方？

南京养老金认证上门服务怎么申请南京市养老金认证

如何评价猪场阉割猪？

最后一个字是豹的成语

泰山散酒怎么样

猫发情的声音(猫发情的叫声)