易坊好文馆

  1. 首页 > 玩科技 >

模拟|Jupyter笔记本实现，慕尼黑工大220页免费书籍介绍基于物理的深度学习( 二 )

模拟 笔记本 方法 智能体 深度 物理 书籍 数值 方程 慕尼黑 Burgers Jupyter


不依赖根据第一性原理精心制作的模型 ， 是否可以通过处理足够大规模的数据集来提供正确答案呢？在这一过程中 ， 将经典数值算法与深度学习技术相结合至关重要 。 其中一个核心原因是深度学习方法非常强大 ， 但同时又可以从物理模型领域知识中获益匪浅 。 深度学习技术和神经网络有时难以应用 ， 而且将我们对物理过程的理解正确地整合到学习算法中通常也非易事 。
过去几十年 ， 研究社区已经开发出高度专业化和精确的离散化方案来求解基础模型方程 ， 如纳维 - 斯托克斯方程（Navier-Stokes）、麦克斯韦方程组（Maxwell's equations）或薛定谔方程（Schroedinger ） 。 与其舍弃在数值数学领域已经开发的强大方法 ， 本书将展示在应用深度学习技术时尽可能多地使用这些方法反而获益颇多 。
书籍概览
本书共分 8 大部分、25 个章节 。 机器之心简单摘取了部分章节的主要内容 ， 更多信息还请参阅原书籍 。
可微物理
本章主要分五个小节：介绍可微物理、具有可微物理梯度的 Burgers 优化、讨论、可微流体模拟、可微分物理与 Physics-informed 训练 。
为了将深度学习和物理模拟更紧密的结合在一起 ， 可以在学习过程中加入可微模拟 ， 简而言之 ， 可称之为可微物理（differentiable physics ， DP） 。 这些方法旨在使用现有的数值求解器 ， 并使其具备根据输入计算梯度的功能 。
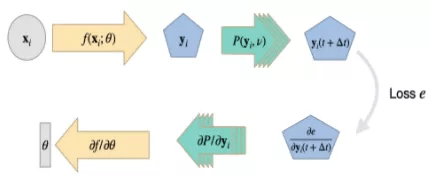
可微物理训练 。

模拟|Jupyter笔记本实现，慕尼黑工大220页免费书籍介绍基于物理的深度学习
文章图片

为了说明在 DP 设置中计算梯度的过程 ， 该小节目标是针对相同的逆问题 ， 使用 Physics-Informed NN 进行 Burgers 优化的 PINN 例子 。
此外 ， 当我们为 DP 方法选择初始离散化时 ， 未知初始状态由相关物理场的采样点组成 ， 我们可以简单地将这些未知表示为浮点变量 。 因此 ， 即使对于初始状态 ， 也不需要设置 NN 。 因此 ， Burgers 重建问题在用 DP 求解时简化为一个基于梯度的优化问题 ， 没有任何神经网络 。
接下来 ， 本章还介绍了一个更复杂的示例 ， 将 Navier-Stokes 方程作为物理模型 。 与「Navier-Stokes Forward Simulation」 一致 ， 用来针对 2D 案例 。
DP 复杂示例
本章主要分四个小节：复杂示例整体概览；利用深度学习减少数值误差、用神经网络求解逆问题以及概述和评论 。
本章给出了更复杂案例的代码示例 ， 以向读者展示通过可微物理训练能够实现哪种任务 。 首先 ， 本章展示了一个使用深度学习来表示数值模拟误差的场景 ， 遵循 Um 等人的建议 。 这是一项基本任务 ， 需要学习模型与数值求解器密切交互 。 因此 ， 这是将数值求解器引入深度学习循环至关重要情况的一个主要例子 。

推荐阅读


上一篇：Google|谷歌将着力解决Git与Laravel等开源项目中的安全问题

下一篇：聂海胜|太空出差三人组终于要回来啦！可老想他们了