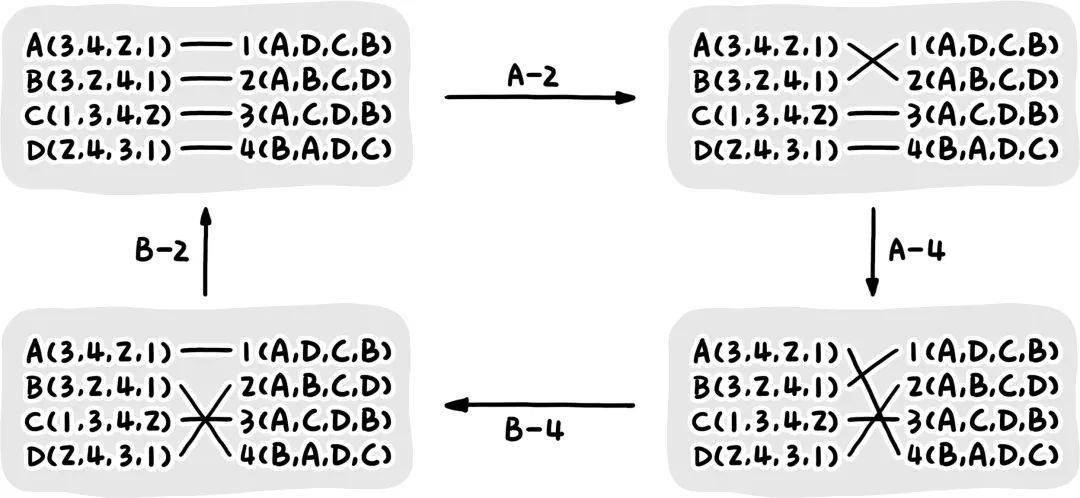
容易看出 , 应用这种“修补策略”所得到的最终结果一定满足婚姻的稳定性 , 但这种策略的问题在于 , 它不一定有一个“最终结果” 。 按照 上述方法反复调整搭配方案 , 最终有可能陷入一个死循环 , 无法得出一个确定的方案(如图 3 所示) 。
文章图片
图 3 应用“修补策略”可能会产生死循环
1962年 , 美国数学家戴维·盖尔(David Gale)和罗伊德·沙普利(Lloyd Shapley)发明了一种寻找稳定婚姻的策略 。
不管男女各有多少人 , 也不管他们各自的偏好如何 , 应用这种策略后总能得到一个稳定的婚姻搭配 。 换句话说 , 他们证明了稳定的婚姻搭配总是存在的 。
有趣的是 , 这种策略反映了现实生活中的很多真实情况 。
在这种策略中 , 男士将一轮一轮地去追求他中意的女子 , 而女子可以选择接受或拒绝相应的追求者 。 第一轮 , 每位男士都选择向自己最心仪的女子表白 。
此时 , 每个女子可能面对的情况有三种:没有人向她表白 , 只有一个人向她表白 , 有不止一个人向她表白 。
在第一种情况下 , 这个女子什么都不用做 , 只需继续等待; 在第二种情况下 , 接受那个人的表白 , 答应暂时和他做男女朋友; 在第三种情况下 , 从所有追求者中选择自己最中意的那一位 , 答应暂时和他做男女朋友 , 并拒绝其他所有的追求者 。
第一轮结束后 , 有些男士已经有女朋友了 , 有些男士仍然单身 。 第二轮 , 每位单身男士都从所有尚未拒绝他的女子中选出自己最中意的 , 并向她表白 , 无论她现在是否单身 。
和第一轮一样 , 每位女子需要从表白者中选择自己最中意的一位 , 拒绝其他追求者 。
注意 , 如果这个女子已经有男朋友 , 当遇到更好的追求者时 , 她必须抛开现任男友 , 投向新的追求者的怀抱 。 这样 , 一些单身男士将会找到女友 , 而那些已经有女友的也可能会恢复单身 。
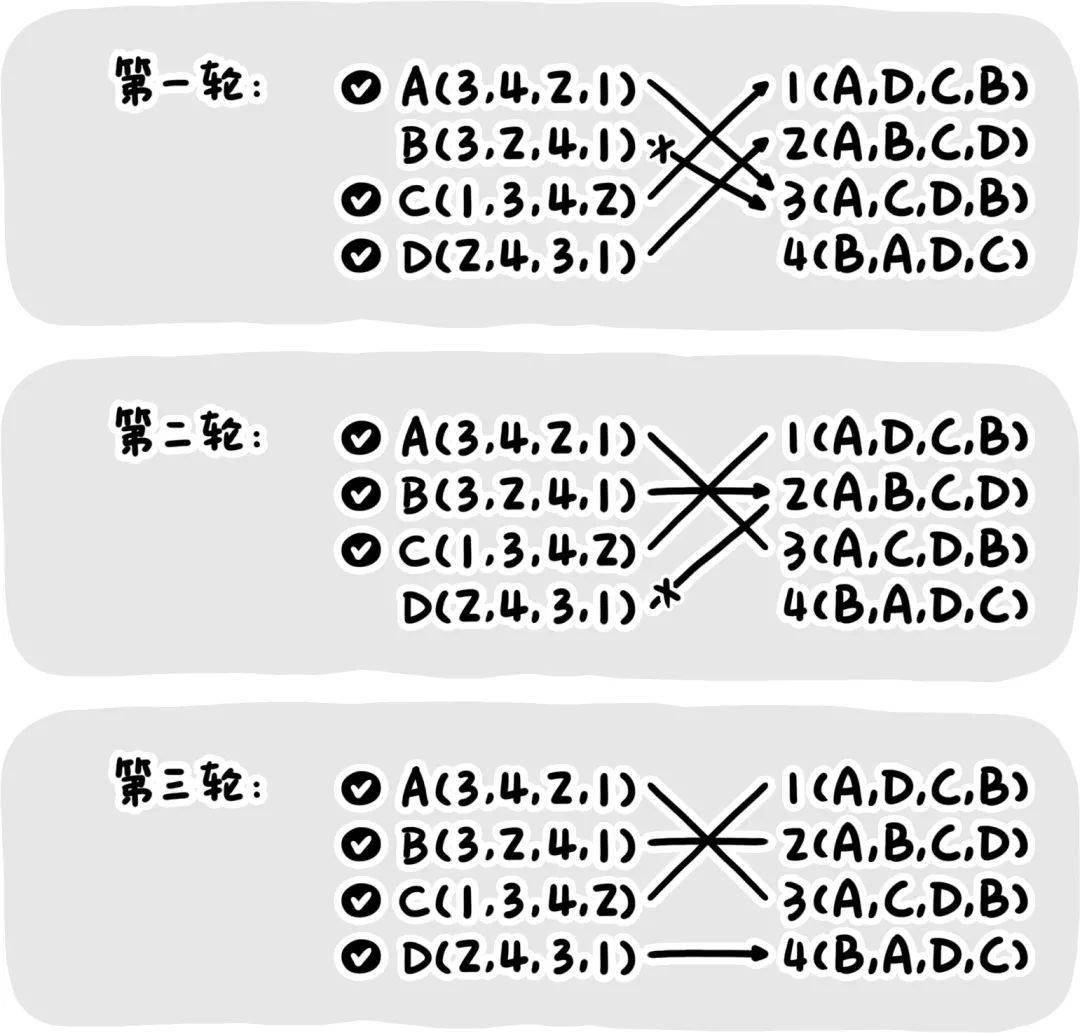
在以后的每一轮中 , 单身的男士继续按照心目中的排序追求下一个女子 , 而女子则从包括现男友在内的所有追求者中选择自己最中意的一个 , 并对其他人说不 。 这样一轮一轮地进行下去 , 直到某个时候所有人都不再单身 , 接下来的一轮将不会发生任何表白 , 整个过程也就自动结束 (如图 4 所示) 。 此时的婚姻搭配就一定是稳定的了 。
文章图片
图 4 应用上述策略 , 三轮之后将得出稳定的婚姻搭配
这个策略会不会像之前的修补法一样 , 出现永远也无法终止的情况呢?
推荐阅读
- 于本|豆瓣 App 安卓新版本 7.20.0 测试
- 苏宁|可循环包装规模化应用 苏宁易购绿色物流再上新台阶
- 产品|泰晶科技与紫光展锐联合实验室揭牌
- 相关|科思科技:无人机地面控制站相关设备产品开始逐步发力
- 生活|数字文旅的精彩生活
- 解决方案|【干货】反渗透设备结垢原因及解决方案
- 解决方案|三菱重工AirFlex:全屋恒温,暖意守护安全工作
- 手机|【直播纪要】VR/MR会吹响消费电子反攻的号角吗?| 见智研究
- 技术|聚光科技旗下临床质谱仪获批医疗器械注册证
- 智能化|龙净环保:智能型物料气力输送系统的研究及应用成果通过鉴定







