混沌方程——产生确定性混沌的最简单的方程，革命性的科学发现动力学

文章图片

文章图片

自然平衡理论认为，如果人类不干预自然，任其自由发展（演变）。最终，自然会达到一种完美的平衡状态。珊瑚礁里总是栖息着数量相近、颜色相同的鱼类；兔子和狐狸会共享土地和林地，狐狸能吃饱的同时，大多数兔子也都能生存下来，种群数量不会爆炸增长或直线下跌。自然将达到一个平衡的状态。直到下一个大陨石，或者超级火山打破平衡。
但事实并非如此。庞加莱指出，行星系统可能是混沌的。行星运动方程中没有明确的随机项，因此在原则上，现在的状态完全决定了未来的状态，但矛盾的是，实际的运动看起来是随机的。

“混沌”与“随机”的含义有很大的不同，混沌与“决定论”相对，混沌中有隐藏的模式（规律）。只有理解了混沌的原因，我们才能从不规则的数据中发现这些模式（规律）。
直到20世纪60年代，数学家、物理学家和工程师才开始意识到混沌在动力学中是多么的普遍。混沌动力学（混沌理论），已经遍布科学的大多数领域。它甚至能告诉我们一些关于经济学和社会科学的事情。混沌理论是微分方程所支配的所有运动的基础，而微分方程是物理定律的基本内容。
生物学中也存在混乱。最早意识到这一点的人之一是澳大利亚生态学家罗伯特·梅(Robert May) 。他试图了解在珊瑚礁和林地等自然系统中，各种物种的数量是如何随时间变化的。 1975年，梅在《自然》杂志上发表了一篇短文，指出通常用来模拟动、植物种群数量变化的方程可能是混沌的。

罗伯特·梅

从混乱理论中得出最重要的结论是，不规则的行为不一定有不规则的原因。以前，如果生态学家注意到一些动物的数量波动很大，他们会寻找一些外部原因。也许是天气的原因，或者是从其他地方突然涌入的捕食者。梅的研究表明，在没有外界干扰的情况下，动物种群的数量变换可能是不规律的，方程为：

k是一个常数，我们可以把k解释为种群数量的增长率

这被称为逻辑斯蒂方程（logistic equation），它是一个动物种群数量的简单模型，每一代的大小由前一代决定。这是一个离散方程，时间单位是“代” ，因此是一个整数。该模型类似于微分方程（时间是一个连续变量），但在计算上更简单。种群数量可以用一个介于0（灭绝）和1（系统可以维持的理论最大值）之间的实数来表示。让时间t按整数步走，对应于“代” 。
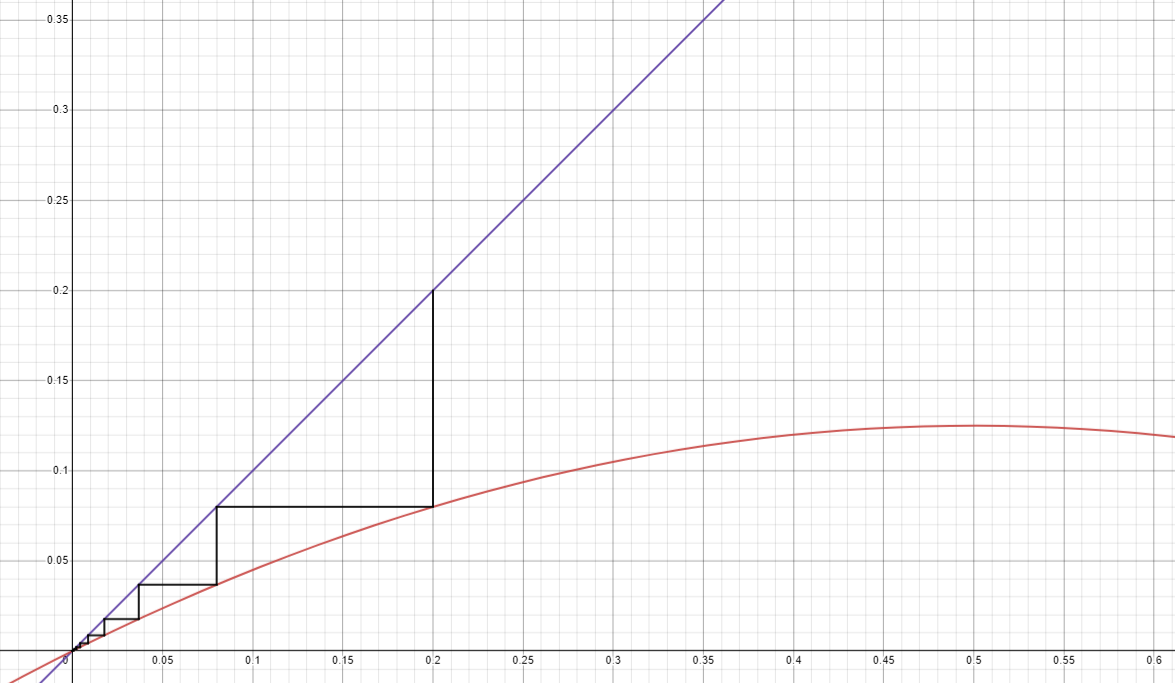
从0时刻开始，总体数量为x_0 。然后我们用t = 0的方程来计算x_1；然后设t = 1 ，计算x_2 ，以此类推。显然，对于任何固定的增长率k ，第0代的种群数量完全决定了后续代的规模。因此，这个模型是确定性的。

x_0=0.2 ， k=0.5时的迭代结果。

那么未来会怎样呢？平衡理论认为，种群数量应该平衡到一个稳定的状态。我们可以计算出这个稳定状态：只要设定t+1时刻的数量与t时刻相同。这样会得到两个稳定状态：0和1-1/k 。大小为0的种群表示已经灭绝（所以应该舍弃）。然而，虽然这是一个稳定的状态，但它也可能不稳定。计算表明，当k大于3时， “稳态”是不稳定的。

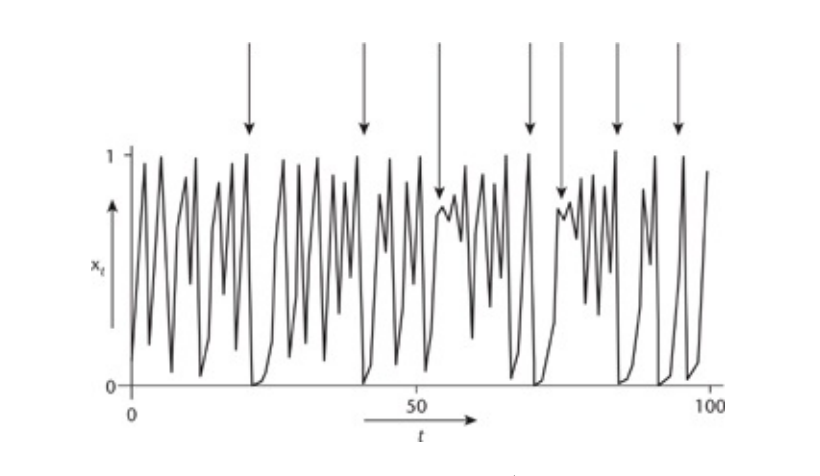
x_0=0.2 ， k=4时的迭代结果。

下图显示了k = 4时种群数量的“时间序列” 。它不是稳定的。然而，如果仔细观察，你就会发现这种动态变化并不是完全随机的。当种群数量变得非常大时，它会立即“跳跃”到一个非常低的值，然后在接下来的两到三代中以一种规则的方式（大致呈指数增长）增长。当种群数量接近0.75时，有趣的事情就会发生：它在该值上下交替振荡，振荡增长形成一个锯齿形，向右变宽（如图中较长的箭头所示）。