
文章图片

文章图片
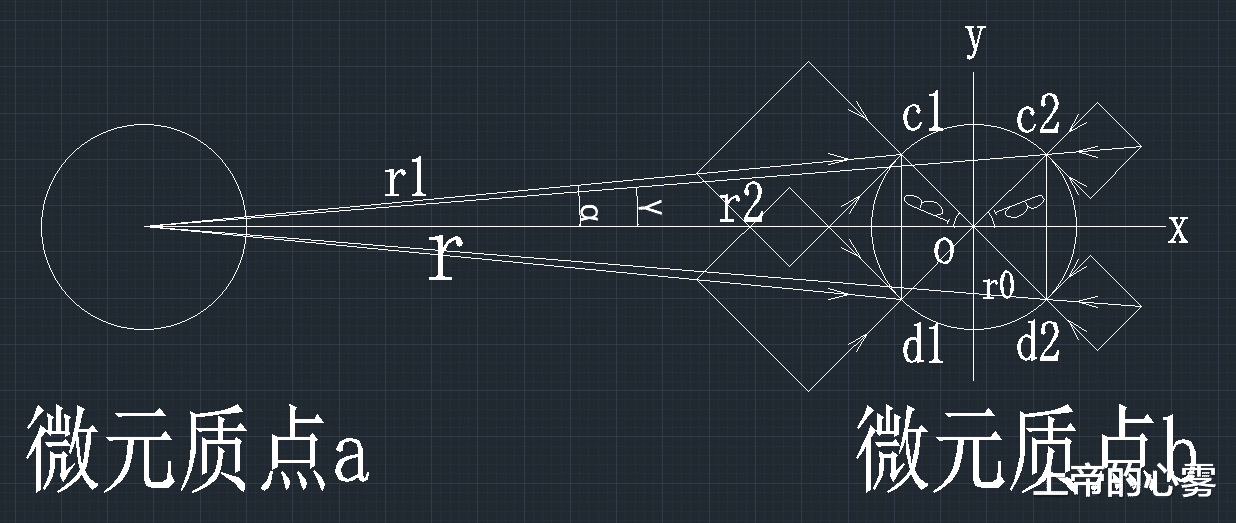
文章图片

文章图片

文章图片
自从发布了磁弦子结构后 , 很久没有花心思在本模型假说上了 , 国庆节时倒是写了篇以太空间的文章 , 但包含内容太多 , 上线后几天又下线了 , 因为雷人的想法比较多 , 可能吓坏了一堆人 , 笑死了一堆人 。
那么 , 我们在这一篇中 , 少放点味道 , 可能比较适合口味清淡的兄弟们 。
本章我们就结合本假说 , 聊一聊一个注明话题:平方反比定律的近似性 。
事先声明 , 该平方反比定律的近似性 , 仅为本假说中存在 , 至于其它定律中是否适用 , 请读者自行思考 , 本人无意冒犯任何人 。
首先 , 我们再次回忆下本假说关于物质本质的假设:
物质性质基本假设
假设一:物质是二元的 。
宇宙中仅存在两种基本纯物质 , 即正物质和反物质 , 该二物质的基本结构单元为球形的正微元质点球(正质点)和反微元质点球(反质点) 。 二者的表面结构强度极高 , 具有现代物理学的刚体性质 , 即使在整个宇宙收缩到极限小体积和极限大压力条件下仍不能被破坏变形 。 宇宙中所有其它物体都由这两种微元质点球组合而成 。
图1 正反两个纯物质的微元质点示意图
注:红色表示正微元质点 , 白色表示反微元质点 。 下同 。
假设二:物质是有限的 。
宇宙中的正反微元质点总数量未知 , 但总数量有限且恒定的 , 正反微元质点数量相等 。
假设三:物质具有当量密度场 , 也称倾向力场 。
每一颗正或反微元质点球 , 都有以自身有限的质量为基础 , 占据无限宇宙空间的倾向 。
或者说:质量是衡量微元质点球占据宇宙空间能力大小的一种量度 。
对于复杂组合物体而言 , 质量就是其正反微元质点总数与基本质量的乘积 。
倾向力场与磁场相似 , 但倾向力场是纯的物质场 , 磁场是正反倾向力场重叠而成的复合场 。
正微元质点的倾向力场与北极磁场同性 , 反微元质点的倾向力场与南极磁场同性 。
图2 微元质点的当量密度场概念示意图
假设四:正反物质遵从同性相斥异性相吸原理
图4 正反两个微元质点的当量密度场相互作用示意图 , 其中最小的红白圆圈表示正反微元质点本身
- 微元质点的当量密度场方程
- 物质基本倾向力场的数学模型
ρ0=m/V0
当假设一个虚拟球体 , 体积可变 , 称为当量体积V当 , 则相应的密度称为当量密度ρ当 , 则当量密度方程:
ρ当=m/V当
由于假设微元质点的当量密度场与当量密度成正比 , 可以写出当量密度场和当量密度的关系式:
E当=G倾ρ当
式中 , E当为当量密度场 , G倾为当量密度场常数 , ρ当为当量密度 。
虽然每一个微元质点的当量密度场都充斥满整个三维的无限宇宙空间 , 但当量密度场和微元质点是一体的 , 仅以微元质点的圆球形界面结构为区别 , 向内为质点本身的真实密度 , 向外则表现为微元质点的当量密度场 。
微元质点的倾向力场方程
根据当量密度场方程:
E当=G倾ρ当=G倾m/V当=(3/(4π))G倾m/r当3)
(4π/3)E当=G倾m/r当3)
建立一个新的倾向力场概念I倾 , 且令:
I倾=G倾m/r当3
可知 , 倾向力场和当量密度场之间的关系为:
I倾=(4π/3)E当
根据方程可知 , 矢量性质的倾向力场概念和标量性质的当量密度场概念在物理内容上是等价的 , 二者的转换系数为4π/3 。
当r=r0 , r0表示微元质点球形界面的本征半径时 , 我们可称此时的倾向力场为微元质点的本征倾向力场 , 密度为本征密度 。







