欧拉常数——最神秘的数字，调和级数的产物，至今看不清它的面貌

文章图片

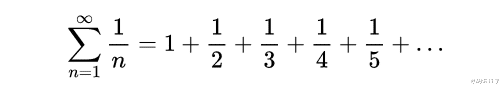
文章图片

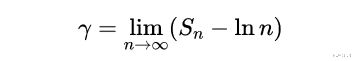
文章图片

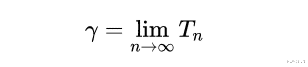
文章图片

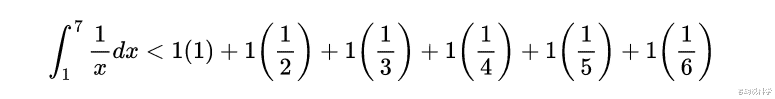
文章图片

文章图片

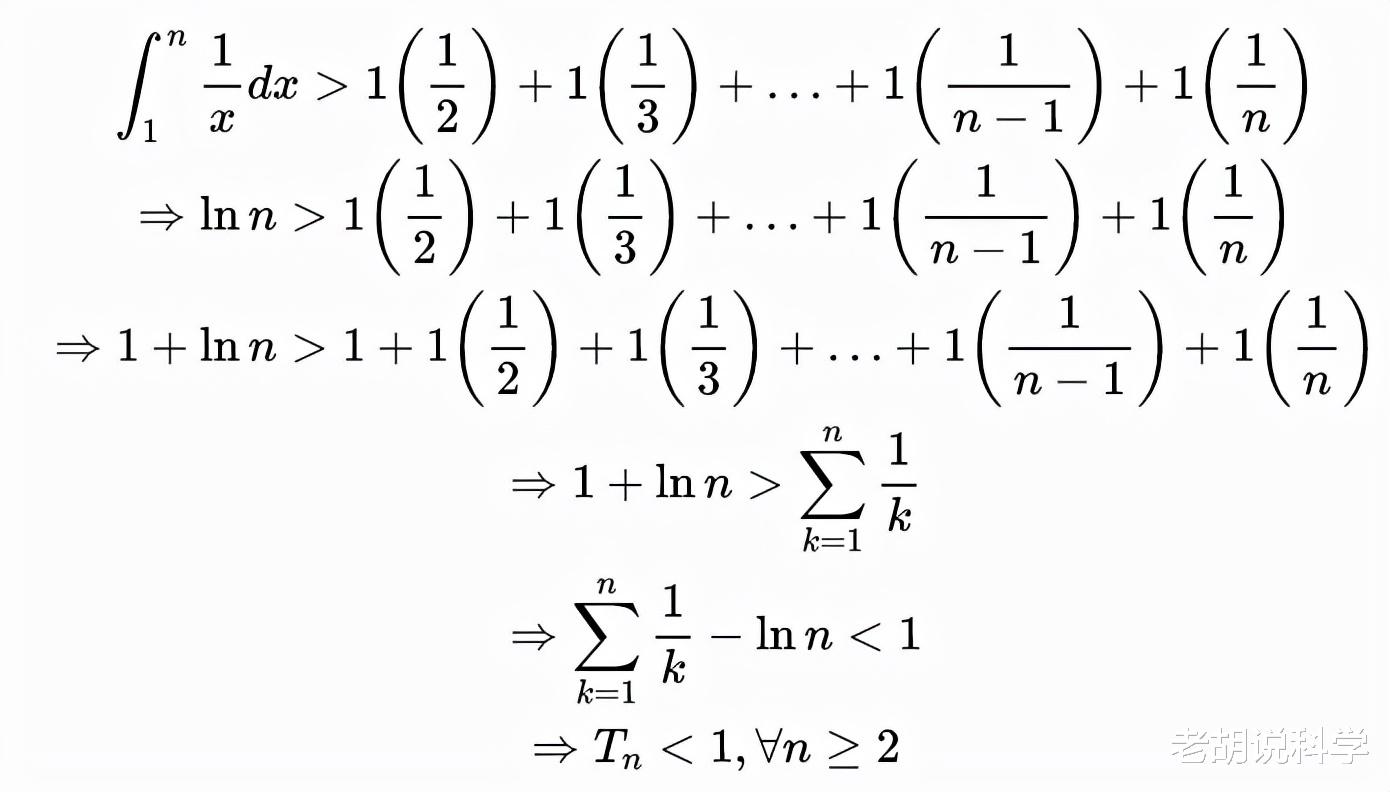
文章图片

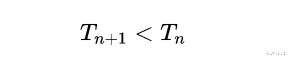
文章图片

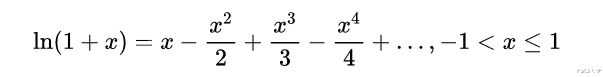
文章图片

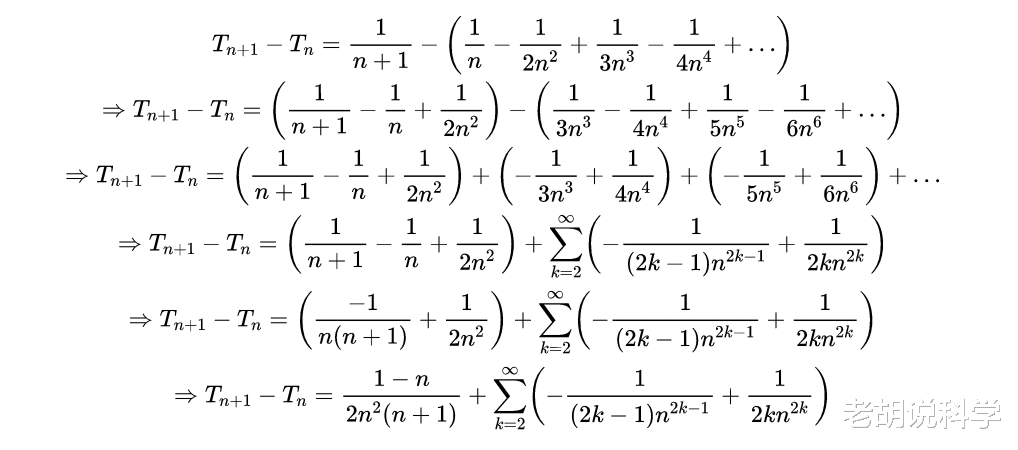
文章图片

文章图片

文章图片

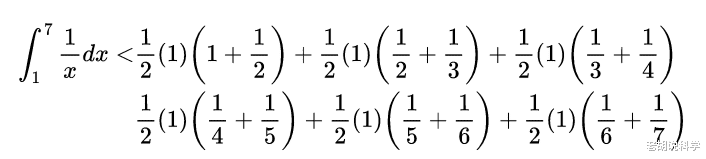
文章图片

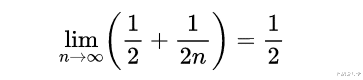
文章图片

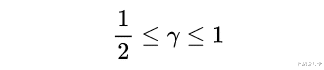
文章图片

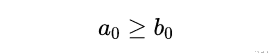
文章图片

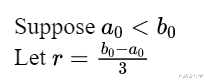
文章图片

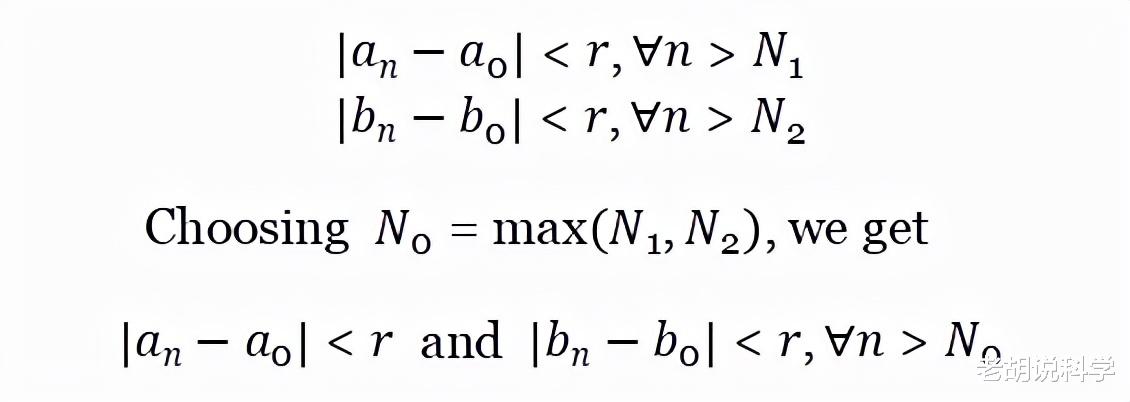
文章图片

还记得调和级数吗？
通常情况下，它是我们遇到的第一个级数，是一个递减级数，但却发散到无穷大。然而，在这篇文章中，我们关注的是这样一个问题：
这里，我们所说的部分和，是指级数的前n项，即：
事实证明，有一个，即自然对数函数。当n变大时，部分和与ln(n)之间的差异接近一个有限的极限。这个极限被称为称欧拉-马斯克若尼常数， γ（gamma）。
该常数首次出现在1734年，其名称来自两位数学家欧拉和意大利数学家马斯克若尼。之所以采用gamma这个符号，很可能是因为这个常数与gamma函数（阶乘函数的延伸）有关。尽管已经存在了近300年，但它是有理数还是无理数一直是个谜。另外， gamma是代数性的还是超越性的也是未知的。
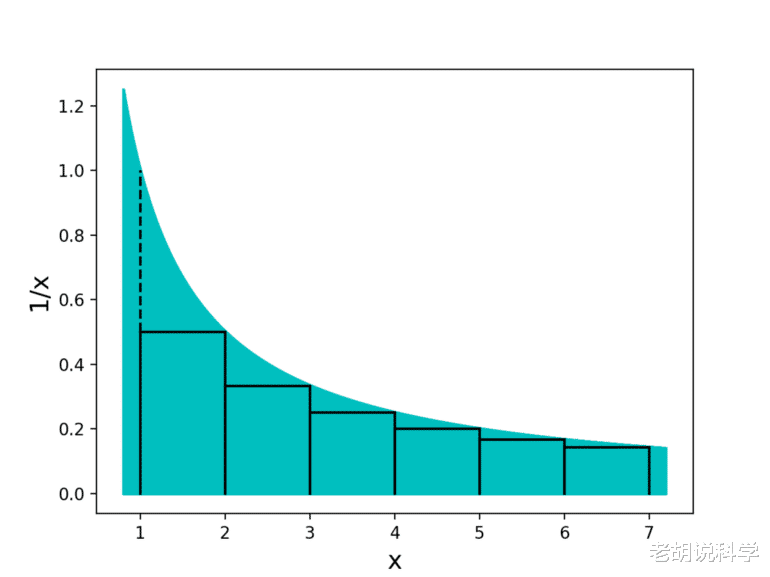
调和数列与对数函数的关系如何？确切地说，这就是本文的内容。接下来的过程依赖于几何直觉，是一个建立良好的级数收敛检验的原型，即积分检验法。
设：
那么：
为了更好地理解，本文分为四个部分：

证明T_n是有界的。
证明T_n是单调递减的，因此，有一个确定的极限，即γ（gamma）存在。

为γ找到一个更严格的下限。
为有兴趣的读者提供一些围绕级数收敛的额外（严格）细节。

T_n是有边界的?首先，我们给出γ的下限。下面是y=1/x的图。在这里，我们利用了一个技巧，即用单位宽度的矩形条比较图下的面积，高度等于函数在该点的值。
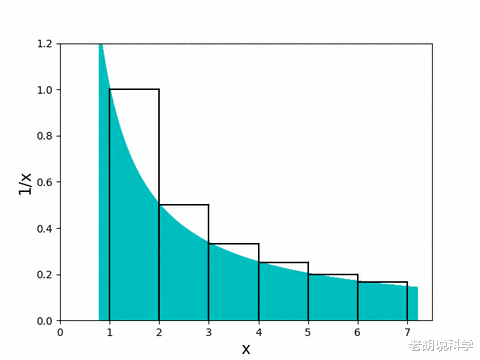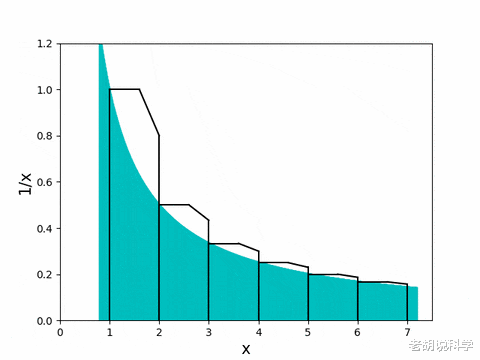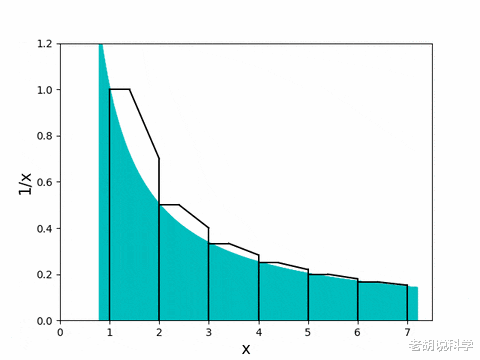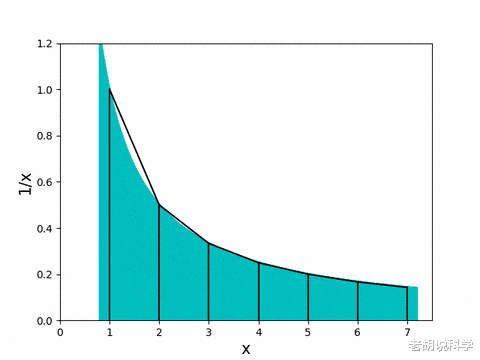
从上述情况可以看出：
推而广之，我们得到：
在证明了T_n自下而上有界后，我们现在继续证明它自上而下也是有界的。之前，矩形的面积主导了曲线下的面积。那么，反过来呢？让我们来看看。