易坊好文馆

  1. 首页 > 玩科技 >

单位|复数背后的直觉——从数学游戏到现实世界( 二 )


单位|复数背后的直觉——从数学游戏到现实世界
文章图片

数学是一种游戏
谈到数字 ， 数学中引入的第一种数字是实数正数 。 我们在我们的小游戏中加入了诸如 "1 "或 "2 "或 "14.5122 "等符号 ， 因为我们看到它们有一个直观的解释 。 它们可以用来描述各种物理物体的数量 。 一个袋子里的苹果数量、一个老人的年龄和一个人的身高就是属于这一类的例子 。 这些符号是许多方程的解 ， 如以下 。
x - 20 = 5
6x - 3.1 = 4
【单位|复数背后的直觉——从数学游戏到现实世界】x^3+ 4 = 5
然而 ， 正实数并不足以描述所有方程的解 。 考虑一下我们游戏中的符号如下：
x+ 6 = 4
使用之前的逻辑规则 ， 没有办法得出一个真正的正解 。 由于我们的游戏中没有一个数学实体来描述这些解 ， 我们将引入一个 。 让我们称它们为负数 。 事实上 ， 只定义一个负数就足够了 ， 其他的就很容易了 。 让我们把 "负数单位 "定义为-1 ， 然后每个负数都等于其正数乘以负数单位 。
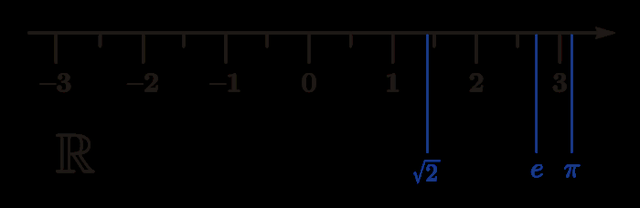
如果真实的正数在几何上可以被看作是一条从0到正无穷的射线 ， 那么负数就只是这条半线向左的延伸 ， 从0到负无穷 。
单位|复数背后的直觉——从数学游戏到现实世界
文章图片

真实线
我们可以用运算正数的方法来运算负数 。 此外 ， 我们可以利用它们的定义来摆脱我们游戏中的整个运算 ， 即减法 。 现在 ， 每当我们看到两个数字的减法时 ， 我们可以用第一个数字的加法和第二个数字的负数来代替它 。
例如 ， 5-3与5+（-3）是一样的 。
我们在很小的时候就接触到 "负数 "的概念 ， 因此我们认为这是理所当然的 ， 但如果你仔细想想 ， 它们根本不是直观的 。 在自然界中没有发现负数 。 你不能说 "那棵树上有负5个苹果" 。 负数是我们在游戏中加入的实体 ， 目的是为了进化游戏 。 然后 ， 我们为它们找到了几种解释 ， 以便在我们的现实世界中使用它们 。
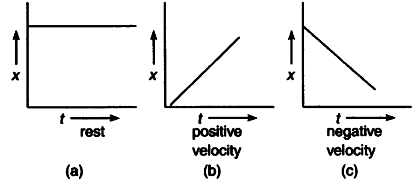
这些解释是什么？嗯 ， 这取决于 。 例如 ， 当我们谈论一个物体的速度时 ， 如果答案是一个负数 ， 那么我们就知道它的运动方向与我们最初假设的方向相反 。 在这种情况下 ， 负数被用来表示方向 。 另一个例子出现在金融领域 。 如果我们正在计算一个企业在一段时间内的总收入 ， 而我们在计算的最后发现了一个负数 ， 那么这意味着这个企业实际上正在亏损 。 在这种情况下 ， 负数表示亏损 。 对负数的解释还有很多 ， 但这两个是最突出的 。
单位|复数背后的直觉——从数学游戏到现实世界

推荐阅读


上一篇：电子|量子力学是如何撑起现代物理学的大厦的？

下一篇：运载火箭|加油，中国航天！航天科技集团2022将有40多次发射任务