易坊好文馆

  1. 首页 > 玩科技 >

单位|复数背后的直觉——从数学游戏到现实世界( 四 )


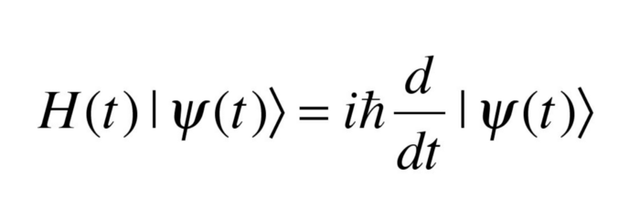
单位|复数背后的直觉——从数学游戏到现实世界
文章图片

量子力学中的薛定谔方程包含虚数单位
尽管复数在现实世界中的直接解释是有限的 ， 但其在数学中的应用是非常重要的 。 复数在许多情况下使数学变得更加容易 。 它们帮助我们描述各种现象 ， 例如以非常简洁的方式描述振荡 。 此外 ， 它们不仅使我们能够更快地解决许多问题（如微分方程） ， 而且使我们能够解决那些我们不可能只用实数对应物来解决的问题 。 虚数和 "实数 "一样真实和有用 。
在本文的最后 ， 我想回答一个你们中的许多人现在可能正在思考的问题 。 既然复数很有用 ， 为什么不发明一种新的数字？首先 ， 有 "更多种类的数" ， 叫作四元数和八元数 ， 但它们远没有复数那么被广泛使用 。 最重要的是 ， 它们是代数封闭的 。 这意味着所有复杂的多项式方程在C中都有解 ， 即复数的集合 。 没有一个多项式方程的解不是复数 。 这被称为 "代数基本定理" ， 它是由卡尔-弗里德里希-高斯证明的 。
单位|复数背后的直觉——从数学游戏到现实世界
文章图片

推荐阅读


上一篇：电子|量子力学是如何撑起现代物理学的大厦的？

下一篇：运载火箭|加油，中国航天！航天科技集团2022将有40多次发射任务